Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Dipolo elétrico

Ver Todos os Exercícios

Teoria

Fala aí, bem vindo ao RespondeAí! Hoje vamos falar sobre Dipolo Elétrico!

O que é um Dipolo Elétrico

Os Dipolos Elétricos são formados por um par de cargas de mesmo módulo, uma positiva e a outra negativa, e essas cargas ficam separadas por uma distância constante entre elas.

Ou seja, um dipolo acontece sempre que você tem uma carga positiva e outra negativa perto uma da outra:

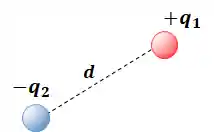
Dipolo elétrico
Dipolo elétrico

Dipolo Elétrico em um Campo Uniforme

Normalmente estudamos dipolos quando eles estão imersos em em campos elétricos uniformes, vamos acompanhar com a figura:

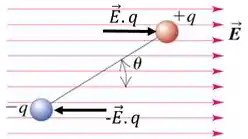
Dipolo elétrico em um campo uniforme
Dipolo elétrico em um campo uniforme

A força que atua na carga positiva possui o sentido oposto à força que atua na carga negativa. Com isso em relação ao movimento de translação teremos um equilíbrio, e o dipolo não irá transladar

Porém como eles irão se manter a uma distância constante e estão livres para se movimentar no campo elétrico, essas forças acabam gerando um torque que atua no dipolo.

Então a tendência desse dipolo é ficar rodando imerso nesse campo uniforme, mas sem transladar.

Torque e momento dipolo

Como essas duas partículas estão sempre afastadas uma mesma distância, podemos considerar que esse sistema está em rotação.

Para calcularmos o torque que atua no sistema precisamos olhar as componentes ortogonais à barra.

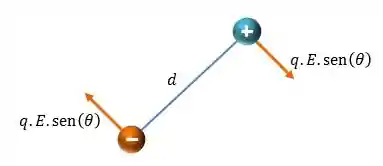
Forças de campo elétrico gerando torque no dipolo
Forças de campo elétrico gerando torque no dipolo

Considerando que a distância entre as cargas valem podemos usar a fórmula do torque para calcular o torque sobre o sistema:’

Aqui temos duas forças com módulo , e a distância de cada força para o centro de rotação é . Assim, o torque resultante nessa barre vale:

Que pode ser reescrito como:

Chamamos de de momento dipolo e ele é representado pela letra .

Dessa forma podemos escrever, que o torque de um dipolo, é produto vetorial entre o momento dipolo e a força do campo elétrico:

Videoaula

Show de bola! Agora vamos ver um videoaula pra garantir que você tá manjando tudo do assunto.

Maneiro né? Acompanha um exercício de dipolos elétricos que nossos Experts prepararam especialmente para você!

Exercícios

No vídeo aqui em baixo você encontra um exercício resolvido passo a passo do tópico de Dipolos Elétricos do RespondeAí, confere os outros no nosso site!

Um dipolo elétrico é formado por cargas e separadas de (). Ele está imerso em um campo elétrico com intensidade de

Aqui no Responde Ai temos um assunto inteiro dedicado a Elétrica que você vai ver nas matérias de Física da faculdade. Olha aqui em baixo e dá uma olhada em vários exercícios pra praticar 👇

Dipolo Elétrico em um Campo Uniforme

Videoaula

Exercícios

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Um dipolo elétrico é formado por cargas + 2 e e - 2 e separadas de 0,78   nm   1 nm = 10 - 9 m . Ele está imerso em um campo elétrico com intensidade de 3,4 × 10 6   N/C .

Calcule a intensidade do torque que age sobre o dipolo quando o momento do dipolo for:

  1. Paralelo ao campo elétrico;
  2. Perpendicular ao campo elétrico;
  3. Antiparalelo ao campo elétrico;

Passo 1

Peraê! Antes de começarmos com as teorias, vamos relembrar a fórmula do torque no dipolo elétrico?

É essa bagaça aqui

τ → = p → × E →

Lembrando que p → é o vetor momento dipolar elétrico, que é um vetor que aponta no sentido saindo da carga negativa e indo para a carga positiva do dipolo. Ah!

p = q d

Pra finalizar, já que estamos interessados somente na intensidade do toque, vale lembrar que, devido ao produto vetorial, podemos escrever

τ = p E sen ⁡ θ

Onde θ é o ângulo formado entre os vetores p → e E → .

Agora podemos seguir com a nossa vida.

Passo 2

a - Paralelo ao campo elétrico;

Bom, se o momento dipolar elétrico for paralelo ao campo elétrico, isso significa que θ = 0 ° , logo:

sen ⁡ 0 ° = 0

τ = 0

Eita, essa foi difícil! :O

Passo 3

b- Perpendicular ao campo elétrico;

Se o momento dipolar elétrico for perpendicular ao campo elétrico, isso significa que θ = 90 ° , logo:

τ = p E sen ⁡ 90 °

τ = q d E sen ⁡ 90 °

Onde:

q = 2 e = 2 × 1,6 × 10 - 19 C = 3,2 × 10 - 19 C

d = 0,78   nm = 7,8 × 10 - 10   m

E = 3,4 × 10 6   N/C

sen ⁡ 90 ° = 1

Vamos lá! Substitui tudo!

τ = 3,2 × 10 - 19 × 7,8 × 10 - 10 × 3,4 × 10 6 × 1

τ ≅ 8,5 × 10 - 22   N⋅m

Passo 4

c - Antiparalelo ao campo elétrico;

Se o momento dipolar elétrico é antiparalelo ao campo elétrico, significa que θ = 180 ° , logo:

sen ⁡ 180 ° = 0

τ = 0

Resposta

a)

τ = 0

b)

τ ≅ 8,5 × 10 - 22   N⋅m

c)

τ = 0

Exercício Resolvido #2

Elaboração Própria

Dado um dipolo de cargas q e – q submetido a um campo elétrico externo E → , Responde Aí:

Qual o ângulo entre o campo e o eixo do dipolo quando o torque é máximo?

Passo 1

Vamos partir pra fórmula do torque então:

τ → = p → × E →

Pra ver quando um vetor é máximo você tem que olhar o módulo dele no olho. O módulo de um produto vetorial é:

τ → = p E s e n θ

Onde θ é o ângulo entre os dois vetores. Naturalmente, pela natureza da função seno:

- 1 ≤ sen ⁡ θ ≤ 1

Então o maior valor que o torque pode assumir é:

τ → = p E

Para os ângulos de:

θ = π 2

θ = 3 π 2

Show?

Resposta

θ ∈ π 2 , 3 π 2

Exercício Resolvido #3

TIPLER, MOSCA, FÍSICA PARA CIENTISTAS E ENGENHEIROS, VOLUME II, 6.ED.

Uma molécula polar tem um momento de dipolo de magnitude 20   e . p m que faz um ângulo de 20 ° com um campo elétrico uniforme de módulo igual a 3 × 10 3   N / C . Determine (a) o módulo do torque no dipolo e (b) a energia potencial do sistema.

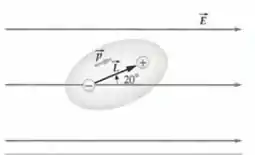
Passo 1

O exercício nos pede o torque no dipolo e também a energia potencial total do sistema certo?

Vamos lembrar as fórmulas. O módulo do torque no dipolo é calculado por

τ = p E s e n ( θ )

A energia potencial do sistema vai ser

U = - p → ⋅ E →

Agora é só a gente substituir os valores nessas fórmulas pra encontrarmos a resposta :D

Passo 2

a) O torque vai ser

τ = ( 20   e . p m ) × 3 × 10 3 × s e n ( 20 ° )

Isso também pode ser escrito assim

τ = 0,02 × 1,6 × 10 - 19 C × 10 - 9 m × 3 × 10 3 × s e n ( 20 ° )

τ = 3,3 × 10 - 27 N . m

Passo 3

b) A energia potencial desse sisteminha vai ser

U = - p E c o s ( θ )

U = - 0,02 × 1,6 × 10 - 19 C × 10 - 9 m × 3 × 10 3 × c o s ( 20 ° )

U = - 9,0 × 10 - 27 J

Resposta

  1. τ = 3,3 × 10 - 27 N . m
  2. U = - 9,0 × 10 - 27 J

Exercício Resolvido #4

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 47-41.

Um elétron está sobre o eixo de um dipolo elétrico a 25   n m de distância do centro do dipolo. Qual é o módulo da força eletroestática a que está submetido o elétron se o momento do dipolo é 3,6.10 - 39 C . m ? Suponha que a distância entre as cargas do dipolo é muito menor que 25   n m .

  • Dado: carga elementar e = 1,6.10 - 19 C

Passo 1

Na figura acima, o elétron está localizado no ponto P e a distância r vale 25 n m . Além disso, o momento do dipolo p = q . d vale 3,6.10 - 39 C . m .

Passo 2

Como a questão diz que d ≪ r , podemos usar a fórmula aproximada:

E = K . p r 3 = 9.10 9 . 3,6.10 - 39 25.10 - 9 3 = 2,0736.10 - 6 N C

Se liga! A dedução dessa expressão do campo gerado por um dipolo está bem explicadinha na teoria.

Passo 3

Multiplicar o campo pela carga para encontrar a força:

F = E . q = E . e = 2,0736.10 - 6 N C . 1,6.10 - 19   C = 3,31776.10 - 25 N

Resposta

F = 3,31776.10 - 25 N

Exercício Resolvido #5

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 45-19.

A figura abaixo mostra um dipolo elétrico. Determina (a) o módulo e (b) a orientação (em relação ao semi-eixo x positivo) do campo elétrico produzido pelo dipolo em um ponto P situado a uma distância r ≫ d .

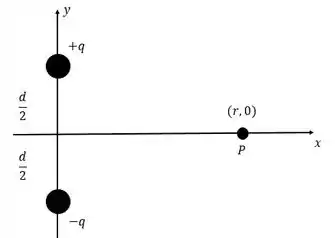
Passo 1

Calcular em função das variáveis o momento dipolo elétrico p :

p = q . d

Passo 2

Exprimir o campo em função do dipolo:

E = K . p r 3 = K . q . d r 3

Passo 3

Se apontarmos os dois campos produzidos pelas duas partículas vamos ter

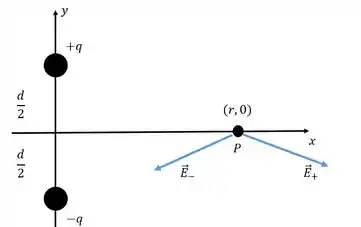
E ao somarmos vetorialmente teremos

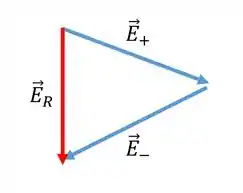
Logo o nosso campo elétrico aponta para baixo! Assim

E → = K . q . d r 3 . ( - y ^ )

Resposta

Logo, o campo elétrico vale:

K . q . d r 3 . ( - y ^ )

Ele aponta para baixo e possui módulo igual a:

K . q . d r 3

Exercício Resolvido #6

UERJ-Física III-Lista de Exercícios sobre Campo Elétrico- n°21.

Quadrupolo elétrico.

A figura abaixo mostra um quadrupolo elétrico.

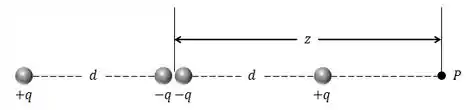
Ele é formado por dois dipolos com momentos de dipolo que são iguais em módulo, têm a mesma direção, mas sentidos contrários.

Mostre que o valor de E sobre o eixo do quadrupolo, para um ponto P a uma distância z do seu centro (suponha que z ≫ d ) é dado por:

E = 3 Q 4 π ε 0 z 4

Onde Q = 2 q d 2 é chamado de momento quadrupolar da distribuição de cargas.

Passo 1

Vamos nessa! Notou que esse desenho é meio diferente do que a gente tava vendo nesse capítulo? Isso porque não tem nenhum triângulo nesse desenho!

E agora? Qual é o campo elétrico de um dipolo gerado nesse caso?

Acompanha comigo. Olha o desenho abaixo:

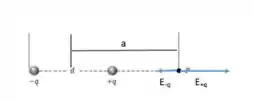
O campo resultante em P mede:

E = E + q - E - q = q 4 π ε 0 a - d 2 2 - q 4 π ε 0 a + d 2 2 = q 4 π ε 0 a 2 . 1 1 - d 2 a 2 - 1 1 + d 2 a 2

Simplificando, temos:

E = q 4 π ε 0 a 2 2 d / a 1 - d 2 a 2 2 = q 2 π ε 0 a 3 d 1 - d 2 a 2 2

Considerando a ≫ d , d a ≪ 1 . Logo, temos:

E = q d 2 π ε 0 a 3

Além disso, dessa vez o campo elétrico tem o mesmo sentido do dipolo. Logo, a fórmula do campo elétrico gerado por um dipolo nesse caso é:

E → = 1 2 π ε 0 p → a 3

p = q d

Onde q é o módulo de uma das cargas, d é a distância entre as cargas e a é a distância entre o ponto médio entre as cargas e o ponto que estamos calculando o campo elétrico.

O momento dipolar elétrico p → é o vetor que aponta da carga negativa para a carga positiva.

Show de bola! O quadrupolo magnético nada mais é do que um arranjo com dois dipolos elétricos, então, o campo elétrico resultando do quadrupolo é o somatório do campo elétrico dos dois dipolos elétricos.

Passo 2

Vamos começar calculando o campo elétrico para o dipolo elétrico mais próximo do ponto P .

Vou adotar o referencial positivo da esquerda para a direita, beleza?

Pra esse dipolo, a distância entre o centro do dipolo até o ponto P é z - d 2 .

Sabemos que o sentido do campo é o mesmo do momento dipolo elétrico (que aponta da carga negativa para a positiva). Como o momento dipolar elétrico está apontando no sentido positivo do eixo x , o campo elétrico para esse dipolo é dado por

E = 1 2 π ε 0 q d z - d 2 3

Passo 3

Agora vamos calcular o campo elétrico para o dipolo mais longe do ponto P .

Pra esse dipolo, a distância entre o centro do dipolo até o ponto P é z + d 2 .

Como momento dipolar elétrico está apontando no sentido negativo do eixo x , o campo elétrico para esse dipolo é dado por:

E = - 1 2 π ε 0 q d z + d 2 3

Passo 4

Por último, agora é só somar os dois e ver qual o campo elétrico resultante:

E = 1 2 π ε 0 q d z - d 2 3 - 1 2 π ε 0 q d z + d 2 3

Tá beleza! Tudo o que fizermos aqui está certo! Então o problema em si acaba aqui... agora é só aquela parte chata de arrumar a equação até ficar igual ao que queremos.

Então agora é na base da disposição!

Vamos começar colocando o que os dois tiverem em comum em evidência, podemos?

E = q d 2 π ε 0 1 z - d 2 3 - 1 z + d 2 3

Bora colocar aquele z do denominador em evidência mas, pra fazer isso, quando tirarmos ele dos parênteses, vamos ter que elevar ele ao cubo.

E = q d 2 π ε 0 z 3 1 1 - d 2 z 3 - 1 1 + d 2 z 3

E = q d 2 π ε 0 z 3 1 - d 2 z - 3 - 1 + d 2 z - 3

Agora é o momento em que você precisa ter fé!

Então fica esperto pro que vamos fazer aqui porque é o único jeito de chegar na fórmula que precisamos...

O que vamos fazer aqui é aplicar a Série de Taylor... vou colocar isso em um próximo passo pra fazer um apelo dramático.

Passo 5

O que é a Série de Taylor? Onde vive? Como se alimenta?

Essas e outras perguntas, responderemos aqui!

A Série de Taylor é uma expansão de uma determinada função em torno de um certo ponto. Beleza, mas como assim?

Então, como, de acordo com o enunciado z ≫ d , você concorda que d vai girar em torno de zero, se compararmos com z ?

É esse o intuito da Série de Taylor, analisar uma função quando ela estiver próximo de um determinado ponto.

A expansão em Série de Taylor de uma determinada função f x em torno do ponto x = a é dada por:

f x = f a + f ' a 1 ! x - a + f ' ' a 2 ! x - a 2 + . . .

Beleza?!

Usando a Série de Taylor nas funções 1 - d 2 z - 3 e 1 + d 2 z - 3 em torno de d 2 z = 0 , teremos o seguinte:

E = q d 2 π ε 0 z 3 1 + 3 d 2 z + … - 1 - 3 d 2 z + …

Agora é só arrumar essa bagaça! ;)

E = q d 2 π ε 0 z 3 2 × 3 d 2 z

E = 3 × 2 q d 2 4 π ε 0 z 4

Onde a 2 q d 2 = Q , logo:

E = 3 Q 4 π ε 0 z 4

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #7

Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exemplo 21.15, pp. 28.

Na Figura abaixo, um dipolo elétrico está centralizado na origem, com o vetor momento de dipolo elétrico  p → apontando para o eixo + O y . Deduza uma expressão para o campo elétrico ao longo do eixo O y , considerando y muito maior do que d .

Use a série binomial 1 + x n = 1 + n x + n - 1 x 2 2 + … , para o caso x > 1 .

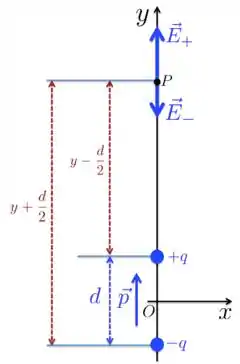
Passo 1

Neste exercício, a gente precisa calcular o campo elétrico resultante | E → R , y | , no ponto P da Figura acima, produzido pelo par de cargas pontuais fixas + q e – q e depois tomar o limite para o obter o valor desse campo resultante quando P tem uma distância y ≫ d . Blz? Vamos lá?

Bom, o módulo do campo elétrico produzido pela carga positiva + q em P é:

E → + = q 4 π ε 0 y - d 2 2     ,

e pela carga negativa – q é

E → - = q 4 π ε 0 y + d 2 2       .

O campo elétrico resultante vai estar na direção do eixo O y e tem módulo dado por

E → R , y = q 4 π ε 0 1 y - d 2 2 - 1 y + d 2 2     .

Tranquilo? O módulo do campo resultante é a diferença entre os módulos: | E → R , y | = E → + - E → - .

Passo 2

Agora, para a gente obter o valor desse módulo para y ≫ d , vamos escrever os termos em que y aparece na última expressão do passo anterior da seguinte forma

1 y - d 2 2 = y - d 2 - 2 = y - 2 1 - d 2 y - 2   .

Tranquilo?? Só isolamos o y e colocamos para fora dos parênteses, OK?

Para usar a expressão da expansão binomial que foi dada, a gente pode fazer x = - d 2 y e n = - 2 lá na naquela expressão do binômio. Com isso, teremos que

1 y - d 2 2 ≈ y - 2 1 + - 2 - d 2 y + - 2 - 1 2 - d 2 y 2 + …   ,

que, reorganizado, fica assim

1 y - d 2 2 ≈ 1 y 2   1 + d 2 y - 3 2 d 2 4 y 2 + …       .

Para o outro termo do campo elétrico resultante | E → R , y | , teremos, de maneira similar ( x = d 2 y e n = - 2 !!), o seguinte

1 y + d 2 2 ≈ 1 y 2 1 - d 2 y - 3 2 d 2 4 y 2 + …   .

Nesse tipo de expansão, a minha sugestão é que você reconheça na expressão que você quer expandir quem é x e quem é n . Depois de fazer isso, vai lá para expressão da binomial e substitui esses termos lá, OK?? Daí não vai ter erro...vai por mim...;-)

Bom, mas ainda não acabou o problema...

Passo 3

Agora precisamos substituir essas duas últimas expansões lá na expressão do campo resultante. Mas, olha só, a gente tem termos do tipo d 2 / ( 4 y 2 ) nessas expressões, correto?

Como y ≫ d

d 2 y 2 ≪ 1 ⇒ d 2 4 y 2 ≪ 1 .

Isso significa que a gente pode desprezar termos dessa ordem na expansões que acabamos de fazer, blz?

Fazendo isso e já substituindo no módulo do campo elétrico resultante | E → R , y | , vamos ter que

E → R , y ≈ q 4 π ε 0 y 2 1 + d y - 1 - d y = q 2 π ε 0 d y 3     .

Como o vetor momento de dipolo elétrico é dado por   p → = q d → , então p → = p = q d , temos

E → R , y ≈ p 2 π ε 0 y 3     .

Agora, dá uma olhada para essa expressão. Diferente do caso do campo elétrico gerado por uma única carga pontual, | E → R , y | depende do inverso da distância ao cubo: 1 y 3 !!! Esse é um comportamento geral do campo elétrico produzido por um dipolo elétrico em pontos a distâncias muito grandes comparadas com a distância entre as cargas + q e – q . Fechou??

IMPORTANTE: Exercícios com expansões como essa que a gente fez aqui são muito comuns, OK? Então, tente reconhecer quais termos da sua expressão são x e n e, depois disso, jogue esses valores lá na expansão binomial para não ter erro, valeu…??

Resposta

E → R , y ≈ p 2 π ε 0 y 3     .

Exercício Resolvido #8

–Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 21.66, Adaptado, pp. 35.

A molécula de água como um todo é eletricamente neutra, porém suas ligações químicas no interior da molécula de água produzem um deslocamente de cargas e o resultado disso é uma carga líquida negativa na extremidade ocupada pelo oxigênio e uma carga líquida na extremidade ocupada pelos hidrogênios, como mostra a Figura a) abaixo. Por isso, molécula assemelha a um dipolo elétrico p → .

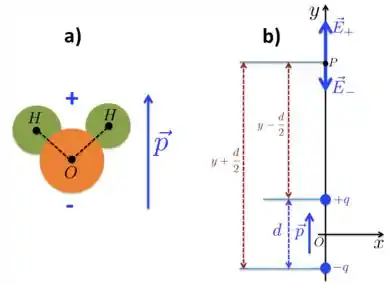
Dada essa situação, suponha agora que o dipolo elétrico da água seja p → = 6,17   ×   10 - 30   C . m e que ele esteja localizado na origem com o momento de dipolo   p → apontando no sentido + y , como mostrado na Figura b) acima. Um íon de cloro ( C l - 1 ), com carga igual a Q = - 1,60   ×   10 - 19   C , está localizado no ponto y = 3,0   ×   10 - 19   m . Supondo que y seja muito maior do que a distância d entre as cargas do dipolo elétrico:

  1. Determine o módulo, a direção e o sentido da força que a molécula de água exerce sobre o íon de cloro ;

  2. A força entre   p → e a carga Q é de atração ou repulsão?

Passo 1

a) Neste exercício, a gente precisa calcular o campo elétrico resultante | E → R , y | , no ponto P da Figura b) acima, produzido pelo par de cargas pontuais fixas + q e – q e depois tomar o limite para o obter o valor desse campo resultante quando P tem uma distância y ≫ d . Blz? Vamos lá?

Bom, o módulo do campo elétrico produzido pela carga positiva + q em P é:

E → + = q 4 π ε 0 y - d 2 2     ,

e pela carga negativa – q é

E → - = q 4 π ε 0 y + d 2 2       .

O campo elétrico resultante vai estar na direção do eixo O y e tem módulo dado por

E → R , y = q 4 π ε 0 1 y - d 2 2 - 1 y + d 2 2     .

Tranquilo? O módulo do campo resultante é a diferença entre os módulos: | E → R , y | = E → + - E → - . Agora, como E → + > | E → - | , o vetor   E → R , y estará apontanto na direção do eixo + O y .

Portanto,

E → R , y = q 4 π ε 0 1 y - d 2 2 - 1 y + d 2 2   y ^   .

Passo 2

Continuação do item a) ....

Agora, para y ≫ d , a gente consegue reduzir essa expressão acima para

E → R , y ≈ p 2 π ε 0 y 3   y ^     .

Substituindo os valores dados no enunciados, temos que

E → R , y ≈ 4,11   ×   10 36 N C   y ^  

Passo 3

b) Portanto, uma carga negativa que está no ponto P sente uma força dada por

F → Q = - Q E → R , y = Q p 2 π ε 0 y 3     - y ^   ,

ou seja, a força sobre Q é de atração e está orientada na direção do eixo – O y .

Com os valores dados no exercício,

F → Q = 6,58   ×   10 17     N   - y ^ .

Resposta

  1. E → R , y ≈ p 2 π ε 0 y 3   y ^ ≈ 4,11   ×   10 36 N C   y ^   ;

  2. F → Q = - Q E → R , y = Q p 2 π ε 0 y 3 - y ^ = 6,58   ×   10 17   N   ( - y ^ )   .

Exercícios de Livros Relacionados

Duas partículas com a mesma carga positiva q são mantidas fixas no eixo y, uma em y =d e a outra em y = - d. (a) Escreva uma expressão para o módulo E do campo elétrico em pontos do eixo x dados por x
Três cargas se situam nos vértices de um triângulo isósceles, como indica a figura 21.43. As cargas de ± 5μ C formam um dipolo.(a) Determine a força (módulo, direção e sentido) que a carga - 10μ C exe
Um dipolo elétrico é submetido a um campo elétrico uniforme E → de módulo 40N/C. A Fig. 22-58 mostra o módulo τ do torque exercido sobre o dipolo em função do ângulo θ entre o campo E → e o momento di
Uma molécula tem um dipolo dado por p → . A molécula está momentaneamente em repouso com p → fazendo um ângulo θ com um campo elétrico uniforme E → . Descreve o movimento subsequente do momento de dip
Um dipolo elétrico que tem momento de dipolo p → está localizado a uma distância perpendicular R de uma linha infinitamente longa de cargas que tem densidade linear uniforme λ . Considere que o moment