Densidade de Carga
Produzido por Bruno SoaresTeoria
Fala aí! Hoje nós vamos aprender sobre densidade de carga de um jeito bem simples e eficaz, tá preparado?
Ah, vale falar que eu vou assumir que você tá sabendo de uns conceitinhos anteriores ao que veremos aqui, beleza? Mas não se preocupa, se tiver precisando de uma revisão bem rapidinha, vou deixar alguns links relevantes aqui pra você 😉
Se liga 👇
- Lei de Coulomb.
- Campo Elétrico Gerado por uma Carga Pontual.
- Resumo de campo elétrico.
- Como resolver uma integral definida?
O que é uma densidade de carga?
De uma forma geral, a densidade de carga é uma medida usada para indicar a quantidade de carga em um comprimento, uma área ou um volume.
Quando começamos a estudar eletricidade em física, tratamos sempre de cargas puntiformes. Mas acontece que, na vida real, lidamos com corpos extensos, que têm comprimento, área e volume. É por isso que precisamos entender como se dá a distribuição de carga nesses corpos, e aí entra a tal da densidade linear, superficial ou volumétrica de carga.
Bora ver mais a fundo cada um desses casos!
Densidade Linear de Carga
Vamos tratar primeiro de corpos unidimensionais, como fios e barras, que têm como única dimensão o comprimento. Nesses casos, teremos uma densidade linear de carga, que nada mais é do que a quantidade de carga que se encontra em cada unidade de comprimento do fio.
Dá só uma olhada nessa imagem:
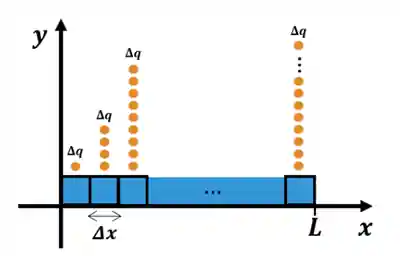
Reparou que cada pedacinho de comprimento
Qual a solução? Pegar um pedacinho muito pequeno do fio, tão pequeno que podemos chamá-lo daquela palavrinha mágica: ✨infinitesimal✨. E aí, já sabe, né? Vamos chamar esse pedaço infinitesimal de
E como isso me ajuda? Olha só, se a gente isolar
E integrarmos os dois lados da equação:
Se aplicarmos a integral definida de
Vamos fazer um exemplo pra garantir que você entendeu.
A barra da ilustração anterior tem um comprimento
Beleza, vamos fazer isso aí que acabamos de falar sobre: aplicar a integral da densidade em relação a
Tranquilo? Então bora para o próximo.
Densidade Superficial de Carga
Aqui, a principal diferença é que teremos um corpo bidimensional. Quer dizer que teremos uma densidade superficial de carga, que é a quantidade de carga que se encontra em cada unidade de área.
A ideia vai ser a mesma, vamos pegar um pedacinho bem pequeno, com área
E, novamente, podemos integrar esse
Nesses casos, o segredo vai ser encontrar quem é esse
Densidade Volumétrica de Carga
Mas não para por aí, ainda podemos ter um corpo tridimensional! Dessa vez teremos uma densidade volumétrica de carga, ou seja, a quantidade de carga que se encontra em cada unidade de volume.
Seguindo o mesmo raciocínio de sempre, nossa densidade volumétrica de carga
E para encontrar a carga total? Só integrarmos para todo o volume!
Agora bora praticar com nossa lista de exercícios resolvidos. Ou se você preferir, dá uma conferida na nossa resolução em vídeo 👇😄
Densidade Linear de Carga
Densidade Superficial de Carga
Densidade Volumétrica de Carga
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Dado um disco de raio com a seguinte distribuição de cargas superficiais:
Qual a carga total?
Passo 1
É o mesmo esquema de sempre, vamos integrar essa parada:
Passo 2
Precisamos agora de uma expressão para o diferencial de área . Como estamos tratando de coordenadas polares, vamos expressar o com respeito à elas.
Seja a área de um disco arbitrário de raio . Temos então que:
Desse fato segue que:
Passo 3
Portanto podemos substituir:
Fim de papo.
Resposta
Exercício Resolvido #2
Elaboração própria.
Uma barra não condutora possui comprimento e carga distribuída uniformemente. Quanto vale a densidade linear de carga dessa barra?
Passo 1
Vamo lá! A gente tem que lembrar antes de tudo que
Então basta substituir os valores dados pelo enunciado e chegaremos no nosso ;D (lembrando de converter o comprimento de centímetros para metros hein)
Resposta
Exercício Resolvido #3
Elaboração Própria
Seja uma esfera de raio e densidade de cargas dada pela expressão
Calcule a carga total na esfera.
Passo 1
Podemos calcular a carga total integrando em toda a esfera as cargas pontuais :
O que corresponde à integrar no seguinte domínio (utilizando coordenadas polares):
Passo 2
Podemos trocar o diferencial de carga por um diferencial de espaço utilizando a definição da densidade:
Substituindo:
Plugando a fórmula da densidade que vem do enunciado:
Passo 3
Agora vamos expressar nosso diferencial de volume em função das coordenadas polares que estamos usando. Seja o volume de uma esfera de raio arbitrário. Desse fato segue que:
Portanto podemos substituir na fórmula:
Fim de papo.
Resposta
Exercício Resolvido #4
Elaboração Própria
Observe a figura abaixo:
Dado que esse anel tem raio , digamos que a densidade de carga linear dele seja:
Onde é o ângulo trigonométrico, medido à partir do eixo no sentido anti-horário e é uma constante arbitrária. A questão é: qual a carga total do anel?
Passo 1
A densidade de carga linear não significa que vamos estar sempre integrando em uma barra reta. Linear significa somente que estamos integrando em uma dimensão só.
Bom, o início do esquema é sempre o mesmo:
Agora integramos em todo o anel:
Show. A função nós temos, agora falta identificar esse e o nosso domínio de integração, que ainda está meio misterioso.
Passo 2
Estamos usando um sistema de coordenadas cartesianas, quem deve ser o nosso ? Seria ou ? Ou nenhum dos dois? Só conseguimos responder isso se entendermos o que de fato é o diferencial de comprimento : ele é um pedaço infinitesimal do anel.
Ou seja, não pode ser nem nem . O único jeito de tratar esse comprimento infinitesimal é com coordenadas polares:
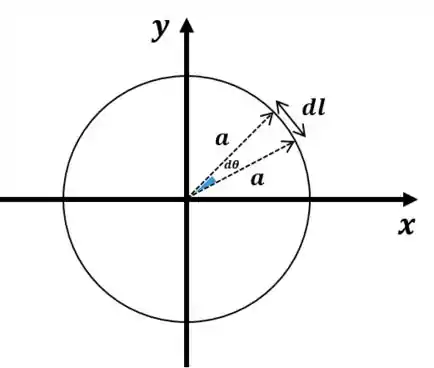
Agora sim, podemos então escrever:
Passo 3
E em função de nós sabemos escrever nosso domínio de integração. Portanto:
Logo:
A carga total deu zero, sendo que ela não é nula em todos os pontos. Pode isso, produção? Claro que pode, ora. Basta que a quantidade de cargas positivas seja igual à quantidade de cargas negativas. Que é exatamente o que acontece. Como podemos observar pela característica da função seno:
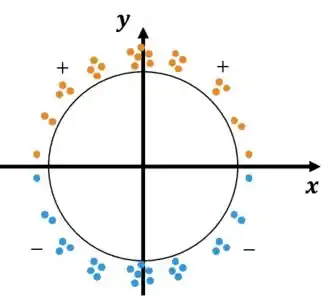
Podemos perceber que a carga total vai dar zero.
Isso encerra como calcular a carga de barras curvas circulares, é só trocar para coordenadas polares.
Resposta
Exercício Resolvido #5
Elaboração própria
Um disco de raio de espessura desprezível tem um furo circular em seu centro. Dado que o raio do furo é e o disco possui densidade de carga superficial igual a:
Com tendo unidades de carga. Calcule a carga total do disco.
Passo 1
Desenhando o que foi descrito temos:
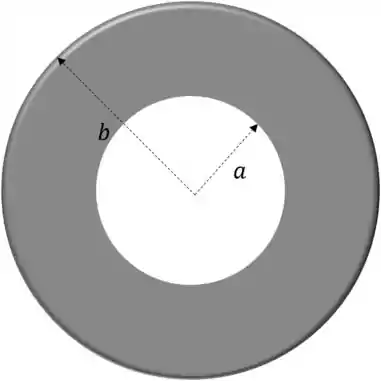
Passo 2
Como queremos a carga total, utilizamos a definição da densidade superficial:
E trocamos o diferencial de área por sua expressão em coordenadas polares. Uma dica para os impacientes (tipo eu): calcule o diferencial com calma. A expressão para a área do círculo você conhece:
Derivando:
E assim evitamos erros crassos, como o que eu acabei de cometer resolvendo essa questão haha.
Passo 3
Integrando em todo o disco:
Segue que:
Puxando o pra fora e arrumando:
Finalmente fazemos a conta da integral:
Arrumando novamente:
Resposta
Exercício Resolvido #6
Elaboração Própria
Uma esfera centrada na origem tem raio e a seguinte distribuição de cargas em seu volume:
Onde é uma constante negativa. Calcule a carga contida no interior de uma superfície esférica imaginária centrada na origem com raio , se:
Passo 1
Desenhando o primeiro caso chegamos à seguinte figura:
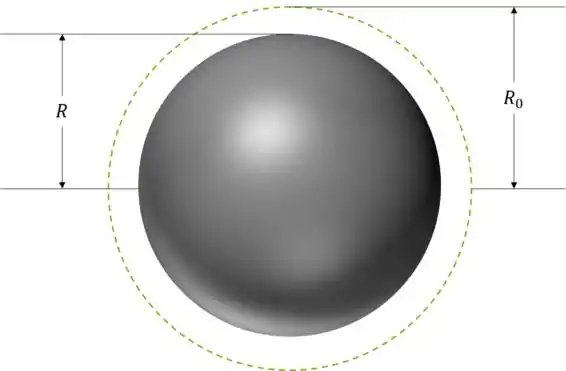
No caso a superfície esférica imaginária está representada somente em corte e com uma linha pontilhada. Não sou sinistro no PowerPoint que nem o Brunão da Física IV.
Passo 2
Do desenho podemos observar que toda a carga que está contida dentro da superfície imaginária é a carga total da esfera, portanto resolvemos o item assim:
Trocando o diferencial de carga utilizando a definição da densidade:
E trocando o diferencial de volume por seu correspondente em coordenadas polares:
Podemos substituir na fórmula e fazer a conta.
Passo 3
Substituindo:
Arrumando:
E finalmente calculamos:
Item respondido!
Passo 4
Agora precisamos desenhar a situação do item :
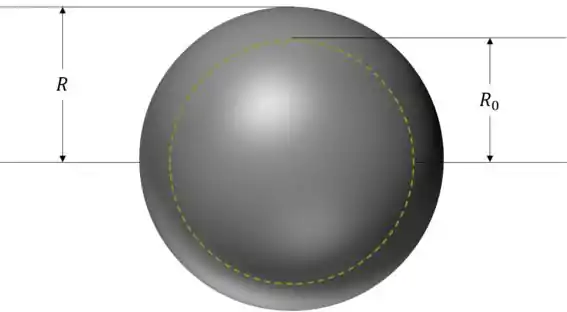
Perfeito. Podemos ver que a carga encerrada no interior da superfície esférica imaginária não é igual à carga total da esfera, e sim um valor menor em módulo.
Como resolver? Somamos apenas os elementos infinitesimais de carga no interior da superfície imaginária:
Pela mesma lógica de antes, substituímos os dados:
E obtemos o resultado:
E acabou.
Resposta
Exercício Resolvido #7
Elaboração própria.
A Figura abaixo mostra uma semicircunferência de raio com uma carga positiva distribuída conforme a seguinte densidade linear , com sendo uma constante. Nessas circunstâncias, qual é a carga total da semicircunferência?
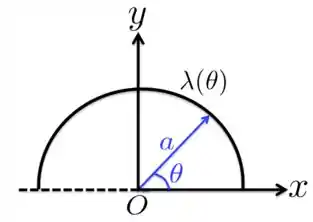
Passo 1
Para encontrarmos o valor da carga total , precisamos resolver a seguinte integral:
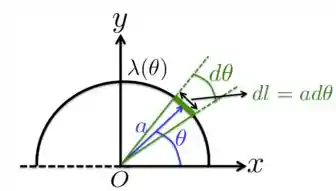
Como mostramos na Figura acima, o elemento de comprimento é dado por . Se substituímos isso na integral juntamente com , ficamos com
Disso, vamos chegar à seguinte expressão para a carga total
Resposta
Exercício Resolvido #8
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 22.65, Adaptado, pp. 70.
Um átomo de hidrogênio é constituído por um próton com carga e um elétron com carga . Podemos considerar o próton como uma carga puntiforme situada em , o centro do átomo. O movimento do elétron faz com que sua carga seja ‘espalhada’ ao longo de uma distribuição esférica em torno do próton, de modo que o elétron seja equivalente a uma carga por unidade de volume dada por
em que é chamado de raio de Bohr.
- Calcule a carga total do átomo de hidrogênio contida em uma esfera de raio centralizada sobre o próton;
- Como fica a carga quando ? Explique o resultado obtido nesse limite.
Passo 1
Neste exercício, temos basicamente o que está representado na Figura a) abaixo. O próton, com carga positiva localizado na origem e a carga do elétron distribuída ao longo de uma esfera de raio com uma densidade de cargas com comportamento exponencial.
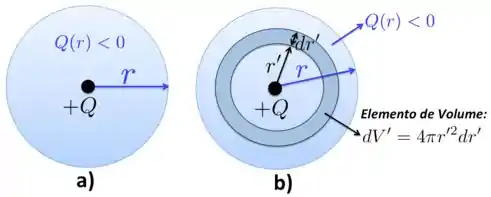
A carga total da Figura a) é dada por
sendo que é a carga ‘espalhada’ do elétron dentro da esfera de raio , que é negativa. Para obtermos a carga total, primeiro vamos calcular a carga do elétron...
Passo 2
a) Para calcularmos , vamos utilizar a Figura b), que mostra um volume ’. Incluindo esse elemento de volume e a densidade volumétrica dada, temos que a carga total é dada por
Como você faz lá no cálculo frequentemente, poderíamos utilizar a integral por partes duas vezes na integral acima e obter o resultado. Aqui, para a gente avançar mais rápido, vou te mostrar o resultado de integrais desse tipo:
em que é uma constante de integração. Aplicando esse resultado em e substituindo os limites de integração, você vai chegar no seguinte:
Somando esse resultando com a carga do próton, a carga total será
Podemos simplicar um pouco mais para obter que:
Passo 3
b) No limite de , como a função exponencial vai a zero mais rapidamente do que as funções de dentro dos parênteses vão para infinito, então, teremos que:
Esse é um resultado esperado, pois se a gente integra sobre todo o espaço, carga total será
que é exatamente a soma das cargas do próton e do elétron, fazendo com que o átomo de hidrogênio seja neutro.
Resposta
- pois o átomo de hidrogênio como um todo é neutro.