Princípio de Pascal
Teoria
Fala aí! Seja muito bem vindo ao Responde Aí! Bora conversar sobre o Princípio de Pascal?
Qual é o Princípio de Pascal?
O Princípio de Pascal, também chamado de Teorema de Pascal, diz que:
“O acréscimo de pressão produzido num líquido em equilíbrio transmite-se integralmente a todos os pontos do líquido”.
-E o que isso quer dizer na prática? 😖
Hoje a gente vai entender tudinho! Se liga nesse vídeo super completo que a gente preparou pra você, sobre o Teorema de Pascal 👇 🧡
📢 Clique para saber mais:
Onde aplicamos o Princípio de Pascal?
O Princípio de Pascal é muito aplicado no nosso dia a dia! Ele esta nos sistemas de amortecedores, prensas hidráulicas, freios hidráulicos e também nos elevadores hidráulicos!
As questões sobre elevadores hidráulicos são clássicas e hoje a gente vai entender de uma vez por todas como o Princípio de Pascal é aplicado aqui!
Elevador Hidráulico
Um elevador hidráulico tem a seguinte aparência:
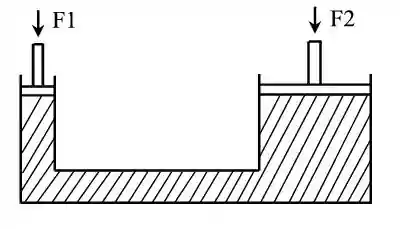
Como podemos ver na imagem acima o elevador hidráulico é um vaso comunicante com dois extremos de áreas transversais diferentes que a gente vai chamar de
Agora, pensando no teorema de pascal podemos deduzir que se eu aplicar uma força na
Lembrando que a pressão é
O êmbolo da
Bora ver como isso fica matematicamente?!
Na figura acima, precisamos de uma força
A pressão aplicada em
E a pressão aplicada em
Bom, mas como a pressão que você aplicou em se propagou por todo o fluido, de acordo com o princípio de Pascal:
Podemos abrir isso:
Mas queremos saber qual é a força necessária para levantar o elevador, então:
E aqui esta o pulo do gato! Não precisamos de uma força
Princípio de Stevin
O Princípio de Stevin diz que:
"A diferença entre as pressões de dois pontos de um fluido em equilíbrio é igual ao produto entre a densidade do fluido, a aceleração da gravidade e a diferença entre as profundidades dos pontos."
Esse enunciado é conhecido como a Lei fundamental da Hidrostática!
Com o teorema de Pascal, calculamos a pressão usando aquela fórmula clássica
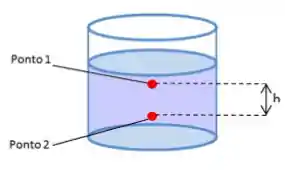
Podemos usar o princípio de Stevin!
Para calcular a diferença de pressão entre os pontos
Onde:
é a diferença de pressão entre os pontos e , em pascal ; é a diferença de altura entre os pontos e , em metro ; -
é a densidade do fluido, em ; é a aceleração da gravidade, medida em .
Agora, bora praticar com exercícios?!
Onde aplicamos o Princípio de Pascal?
Princípio de Stevin
Exercícios Resolvidos
Exercício Resolvido #1
Instituto Federal de Educação, Ciência e Tecnologia, SP, Prof. Luiz Rodrigues
A prensa hidráulica mostrada na figura está em equilíbrio. Sabendo-se que os êmbolos possuem uma relação de áreas de , determine a intensidade da força .
Passo 1
Temos uma prensa hidráulica em equilíbrio.
Então, aplicaremos o Princípio de Pascal:
As pressões são iguais em cada extremidade:
Logo:
Passo 2
Conhecemos as relações entre as áreas nos dois lados:
No lado esquerdo, sabemos a força aplicada:
Observação: mesmo que a gente não conheça essa unidade de força, isso não influencia nas contas. No final, encontraremos nessa mesma unidade!
Passo 3
Substituindo fórmulas:
Rearranjando:
Passo 4
Substituindo valores:
Resposta
Exercício Resolvido #2
Elaboração própria
Um objeto de peso é colocado sobre a área maior de um elevador hidráulico que possui valor de . Determine a mínima força necessária a ser aplicada sobre a área menor, de valor , para que o objeto possa ser elevado.
Passo 1
Nós só temos que encontrar uma força que compense a força peso do objeto sobre a área maior. Pelo princípio de Pascal:
Resposta
Força mínima que deve ser aplicada vale .
Exercício Resolvido #3
Halliday, Vol 2, Capítulo 14, 9ª edição, exercício 28, página 82
Um êmbolo com uma seção reta é usado em uma prensa hidráulica para exercer uma pequena força de módulo sobre um líquido que está em contato, através de um tubo de ligação, com um êmbolo maior de seção reta .
(a) Qual é o módulo da força que deve ser aplicada ao êmbolo maior para que o sistema fique em equilíbrio?
(b) Se os diâmetros dos êmbolos são e , qual é o módulo da força que deve
ser aplicada ao êmbolo menor para equilibrar uma força de aplicada ao êmbolo maior?
Passo 1
(a) Queremos para que o sistema fique em equilíbrio. Bom, pelo princípio de Pascal a gente tem que a pressão exercida no êmbolo menor é igual a exercida no êmbolo maior e a pressão é dada por:
Logo, igualando as pressões no êmbolo menor e no maior:
Isolando a força :
Passo 2
(b) Vamos usar o princípio de Pascal de novo!! Na verdade a situação dessa letra é bem parecida com a da letra (a), só que agora nós queremos a fórmula para a força no êmbolo menor e temos os valores para substituir na fórmula encontrada e fazer as contas!
Pelo princípio de Pascal, vimos que:
Agora, isolando :
Passo 3
Beleza! Agora, vamos calcular essas áreas!
Lembrando que a área das seções será dada pela área do círculo:
Como o diâmetro do êmbolo menor é , o raio será e, então, sua área .
Como o diâmetro do êmbolo maior é , o raio será e, então, sua área A.
Além disso, vamos ter que a força sobre o êmbolo maior vale .
Passo 4
Show! Dessa forma, podemos substituir os valores encontrados na fórmula que encontramos para no passo 2:
E calculando esse cara aí, chegamos que:
Resposta
Exercício Resolvido #4
Instituto Federal de Educação, Ciência e Tecnologia, SP, Prof. Luiz Rodrigues
Na figura apresentada a seguir, os êmbolos (A) e (B) possuem áreas de e respectivamente. Despreze os pesos dos êmbolos e considere o sistema em equilíbrio estático. Sabendo-se que a massa do corpo colocado em (A) é igual a , determine a massa do corpo colocado em (B).
Passo 1
Queremos determinar a massa do bloco em (A) para que o sistema permaneça em equilíbrio.
Temos uma prensa hidráulica. Então, aplicaremos o Princípio de Pascal.
As pressões são iguais nas duas extremidades:
Passo 2
Conhecemos as áreas nos dois lados:
No lado esquerdo, a força aplicada é igual ao peso do bloco de :
onde .
E, no lado direito, a força aplicada é igual ao peso do outro bloco:
Passo 3
Agora é hora de substituir as equações dos passos anteriores:
Passo 4
Vamos substituir os valores. Repara que, como a gente tem uma razão entre duas áreas, a gente não precisa converter de pra . A gente só precisa garantir que as duas tenham a mesma unidade.
Resposta
Exercício Resolvido #5
Elaboração própria
Considere uma prensa hidráulica. Qual deve ser a relação entre os diâmetros para que a força de um lado seja igual a um quarto da força no outro lado?
Passo 1
Como as pressões são iguais, temos que
Logo:
E isso é equivalente a:
Queremos que a relação entre as forças seja . Logo:
Substituindo na igualdade acima, encontramos as relações entre as áreas:
Passo 2
A área do círculo é dada por .
Substituindo na relação entre as áreas:
Como a razão tem que ser positiva, podemos tirar a raiz nos dois lados:
Sendo o diâmetro o dobro do raio, podemos multiplicar por em cima e embaixo:
Logo:
Resposta
Exercício Resolvido #6
Hugh D. Young e Roger A. Freedman, Física II – Termodinâmica e Ondas, 12a ed. São Paulo: Addison Wesley, 2008, pp 95
No elevador hidráulico mostrado na figura qual deve ser a razão entre o diâmetro do braço do recipiente sob o carro e o diâmetro do braço do recipiente onde a força é aplicada para que um carro de possa ser erguido com uma força de apenas
Passo 1
Bom galera, aqui nós vamos usar a fórmula:
Como o enunciado está pedindo a razão entre os diâmetros, precisamos achar uma relação entre as áreas.
Passo 2
Bom, mas pra achar uma relação entre as áreas, a gente precisar primeiro calcular as forças que atuam em cada pistão do elevador hidráulico.
A , a força que será aplicada pra se erguer o carro, vale . O enunciado já nos disse.
E a outra força? Bem, essa é força peso do carro.
Então:
Passo 3
Então já podemos usar a equação:
Passo 4
Show, mas essa é a razão entre os diâmetros? Ainda não!!!!
Como a área de um círculo é dada por:
E como o raio é metade do diâmetro:
Assim:
Assim:
Sacou? Só manipulei a equação simplificando os termos iguais e chegando numa razão para os diâmetros.
Então:
Resposta
Exercício Resolvido #7
Halliday, Vol 2, Capítulo 14, 9ª edição, exercício 29, página 82
Na figura abaixo, uma mola de constante elástica liga uma viga rígida ao êmbolo de saída de um macaco hidráulico. Um recipiente vazio de massa desprezível está sobre o êmbolo de entrada. O êmbolo de entrada tem uma área e o êmbolo de saída tem uma área 18,0A. Inicialmente, a mola está relaxada. Quantos quilogramas de areia devem ser despejados (lentamente) no recipiente para que a mola sofra uma compressão de ?
Passo 1
Pelo princípio de Pascal, nós temos que:
Passo 2
Aqui vai uma observação: a força exercida sobre o êmbulo maior é justamente a força elástica () pela mola e a força exercida sobre o êmbulo menor será a força peso (), à medida que o recipiente for preenchido. Então:
Onde é a deformação da mola e vale , e . Com isso:
Resposta
Devem ser despejados de areia.
Exercício Resolvido #8
UERJ-LISTA-MF-9
Numa prensa hidráulica, um pistão, cuja seção transversal tem área , exerce uma pequena força no líquido contido na prensa. Este líquido passa através de um tubo para outro recipiente de área , conforme a figura abaixo:
Determine a força que o pistão maior deve suportar
Se o pistão menor tiver um diâmetro de e o diâmetro do pistão maior for igual a , que peso deve ser colocado sobre o pistão menor para que o pistão maior possa suportar uma massa de toneladas?
Calcule a distância percorrida pelo pistão maior para que o pistão menor se eleve até uma altura de .
Passo 1
Bem, aqui vamos usar o famoso Princípio de Pascal! Primeiramente, devemos encontrar uma relação entre as forças atuantes em cada pistão e suas áreas. Então, vamos lá:
O Princípio de Pascal nos diz que as pressões nos dois pistões serão iguais, já que ambos estão na mesma altura. Logo:
Queremos determinar Logo, basta que manipulemos a equação acima. Assim, a força que o pistão maior deve suportar é dada pela expressão:
Passo 2
Estamos agora numa situação parecida com a , só que agora temos que achar . Vamos ver quais informações nós temos:
Massa que será colocada sobre o pistão maior: Diâmetro maior : Diâmetro menor:
Vamos primeiro calcular
Essa força nada mais é do que o peso que será posto sobre o pistão, logo, sabendo a massa e usando :
Vamos calcular agora as áreas das extremidades dos pistões, lembrando de usar a metade dos valores dos diâmetros (raios):
Logo, será:
Passo 3
O pulo do gato para resolver essa opção é levar em consideração que o volume deslocado por um pistão tem que ser o mesmo deslocado pelo o outro, já que o fluido é incompressível. Logo:
Diâmetro maior : Diâmetro menor:
Sendo e :