Conservação de Energia
Produzido por Ludovic BeghinTeoria
Introdução
Você já deve ter ouvido falar dos satélites que orbitam os planetas, já se perguntou porquê eles simplesmente não caem na terra com frequência ou desviam sua órbita?
O motivo dos satélites manterem essa órbita é que a energia se conserva também nas órbitas circulares e isso acontece por quê a força que atua no satélite é a força gravitacional que é conservativa.
Como a energia se conserva o satélite mantém sempre o mesmo movimento, e por isso não sai de órbita ou simplesmente cai na terra. Por isso podemos aplicar o teorema da energia mecânica aqui.
Pô, moleza a energia potencial gravitacional a gente já aprendeu a calcular e a energia cinética é só fazer:
E jaera, problema resolvido né?

E se eu te disser que nesses problemas você não terá a velocidade do satélite? Nesses casos, como calcular essa energia cinética?

Vem comigo que vamos aprender juntos um novo jeito da gente calcular essa energia!
Conservação de Energia em Órbitas Circulares
A conservação em si é a mesma que você já aprendeu. Pegando dois instantes diferentes, sabemos que:
E, portanto:
Onde é a energia gravitacional e é a energia cinética.
Aqui o que muda é a forma de calcular cada uma das energias, lembra da energia gravitacional?
Já vimos que sua expressão é:
Onde e são as massas dos corpos, é a constante gravitacional e é a distância entre os corpos que nesse caso é o raio da nossa órbita circular.
E a energia cinética a gente encontra a partir do clássico.
Porém como estamos falando de órbitas circulares temos aí um movimento circular onde a resultante da força que aponta para o centro do movimento é a força centrípeta.
E se olharmos para o movimento vamos ver que a força gravitacional aponta para o centro da Terra.
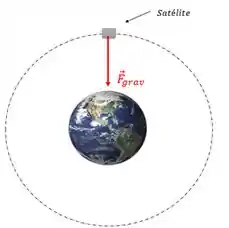
Lembrando que a força gravitacional é dada por:
Mas pera aí, a força gravitacional nesse caso é igual a força centrípeta.
Essas relações só são válidas para órbita circulares!
Podemos reescrever a energia cinética como:
E aqui encontramos a nova expressão pra energia cinética das órbitas circulares, se ligou?
Se compararmos a energia cinética com a gravitacional poderemos ver o seguinte:
Como a energia mecânica é a soma das energias temos:
E como a energia se conserva, ela será sempre constante mantendo o raio da órbita constante e por isso o satélite não sai de órbita.
Lembrando que essas relações só são válidas para órbita circulares!
Em alguns casos raros um satélite cai na terra ou se afasta da órbita, porquê isso acontece se a energia se conserva?
Variação de Energia
Imagina que o satélite de antes se afastou da terra aumentando o raio da órbita pra , o que aconteceu no processo?
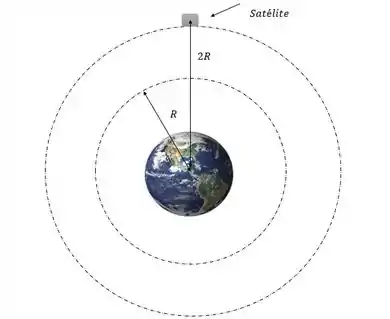
Houve um afastamento do satélite, mas isso é possível dado que a energia se conserva?
A energia mecânica inicial é a qual foi calculada:
A energia mecânica final também pode ser calculada como sendo
Então a energia mecânica final agora é a metade da anterior, mas isso é possível?

Bom é possível se por algum motivo o satélite receber ou ceder energia então nesse caso a energia não vai se conservar e será gerado trabalho.
Para sair da órbita e ir para uma nova órbita foi necessário a realização de trabalho e podemos calcular esse trabalho fazendo:
Como o trabalho é positivo, foi acrescentado energia ao sistema, ou seja, para sair da órbita de raio R para uma órbita de raio 2R, foi necessário realizar esse trabalho. Esse caso funciona como um propulsor que insere energia no sistema.
Caso desse um trabalho negativo (ocorre quando a órbita diminui de raio), aí seria o caso em que se tirou energia do satélite (como um freio).
Por fim pra gente recapitular, trouxe uma tabelinha com as equações de cada energia e na linha mais abaixo as energias em função da potencial
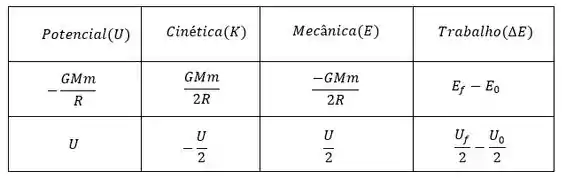
E é isso o que precisamos saber sobre esse assunto, bora pros exercícios??