Velocidade de Escape
Produzido por Ludovic BeghinTeoria
Fala aí! Seja bem vindo ao Responde Aí! Bora conversar sobre Velocidade de Escape?
O que é Velocidade de Escape?
A velocidade de escape é a velocidade necessária para que um objeto, lançado da superfície de um planeta ou outro corpo qualquer, atinja uma distância grande o suficiente para que o deixe de haver interação entre eles.
A velocidade de escape da terra é igual a
Como Calcular a Velocidade de Escape
Pra a gente calcular a velocidade de escape, usamos a seguinte fórmula:
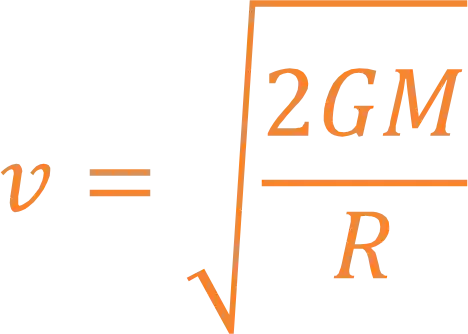
Onde
📢 Clique para ver mais:
Fórmula da Velocidade de Escape: Demonstração
Agora bora entender da onde saiu essa fórmula da velocidade de escape?! Então se liga nesse videozinho super completo que o Responde Aí preparou pra você! 👇
Ou continua comigo no textinho!
Pra a gente chegar na fórmula da velocidade de escape, vamos supor a situação da imagem a seguir: um corpo de massa
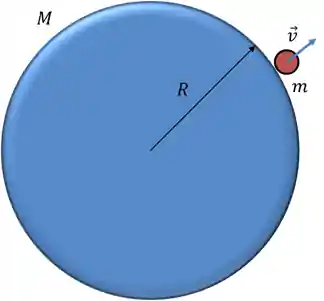
A energia do sistema nesse instante é dada por:
Suponha agora um instante posterior, onde a massa m alcance uma distância tão grande que a energia potencial gravitacional seja zero. Como estamos procurando a velocidade mínima para que isso ocorra, suponha que neste mesmo instante a velocidade do corpo é zero.
Com isso, temos, para a energia neste instante:
Então agora nos basta usar o princípio da conservação da energia, resultando em:
Isolando a velocidade, chegamos em:
Prontinho!
Exercícios Resolvidos
Exercício Resolvido #1
Randall D. Knight, Física Uma Abordagem Estratégica – Volume 1, 2a ed. Porto Alegre: Bookman, 2009, pp 396 – Exemplo 13.2
Um foguete de é lançado em linha reta a partir da superfície da Terra. Que valor de velocidade o foguete necessita ter para “escapar” da atração gravitacional da Terra e jamais voltar? Considere uma Terra desprovida de rotação.
Passo 1
Vamos pensar juntos. O foguete vai pra bem longe da Terra, certo? Então a força gravitacional vai ser baixíssima, tendendo a zero. Sendo assim, a forma de calcular essa velocidade fica sendo a partir da energia, cujo valor é zero no infinito.
É fácil pensar desse jeito. É só analisar o enunciado, se o corpo está “fugindo” da Terra, velocidade calculada por energia. Se o corpo está do ladinho da Terra fielmente, velocidade calculada pela força resultante de rotação.
Passo 2
Que comecemos os trabalhos com a conservação da energia.
Ou,
Resposta
Exercício Resolvido #2
TIPLER, P., MOSCA, G. Física para Cientistas e Engenheiros, Vol. 1, 6ª Ed, LTC, 2009, p. 398 ex. 11.
Suponha que a rapidez de escape de uma planeta seja apenas levemente maior do que a rapidez de escape da Terra, apesar de o planeta ser consideravelmente maior do que a Terra. Como se compara a massa específica(média) do planeta com a massa específica(média) da Terra?
- Deve ser maior
- Deve ser menor
- Deve ser igual
- Não se pode determinar a resposta com os dados fornecidos
Passo 1
Vamos relembrar a fórmula para velocidade de escape:
Assim, a velocidade de escape da Terra é dada por:
E a velocidade de escape do outro planeta é dada por:
Passo 2
Dividindo as velocidades de escape do planeta e da Terra, temos:
Considerando o planeta e a Terra esféricos, temos:
Substituindo na razão entre as velocidades, temos:
Passo 3
Considerando que seja quase igual a :
Como :
Resposta
Letra b.
Exercício Resolvido #3
UNICAMP-P1-2010-Q2 b
Considere um projeto de lançamento onde satélites são lançados como projéteis. Seja a constante gravitacional, e e , o raio e a massa da Terra, respectivamente.
(a) Ignorando a atmosfera e a rotação terrestre, deduza a velocidade com que um projétil deve ser lançado para atingir uma altitude máxima de medida a partir da superfície.
(b) Calcule a razão entre a velocidade de escape de um satélite lançado da Terra e a velocidade de escape do satélite lançado de um planeta cujo raio vale e cuja massa é
Passo 1
a)
A partir da conservação de energia temos que:
Isolando a velocidade:
Fazendo o MMC:
Passo 2
b)
Por conservação de energia:
Podemos deduzir a fórmula da velocidade de escape:
Na Terra:
Calculando a velocidade de escape num planeta arbitrário:
Temos então que a razão é:
Resposta
a)
b)
Exercício Resolvido #4
USP-P3-2015-6
No topo de uma montanha na Lua, um projétil é disparado horizontalmente com a velocidade (velocidade de escape),onde é a distância do topo da montanha ao centro da Lua, é a massa da Lua e é a constante de gravitação universal. Neste caso, desconsiderando a contribuição da Terra e do Sol para o campo gravitacional, o qual a curva que descreve a trajetória do objeto?
a) Uma parábola ou uma hipérbole, se afastando da Lua.
b) Uma parábola, caindo na superfície da Lua.
c) Uma elipse.
d) Um círculo.
e) Uma reta.
Passo 1
O fato de ser na Lua ou em qualquer planeta não muda em nada as contas.
A velocidade de escape é a velocidade necessária para um corpo escapar do campo gravitacional de um planeta. Daí, se não houver atrito algum, com essa velocidade a tendência é sair de órbita.
Passo 2
A órbita de escape de um objeto é geralmente de forma parabólica se afastando do solo.

Resposta
a) Uma parábola ou uma hipérbole, se afastando da Lua.