Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.6 - Ex. 24
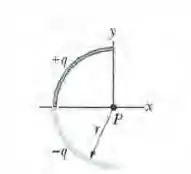
Na Fig. 22-44, uma barra fina de vidro forma uma semicircunferência de raio . Uma carga está distribuída uniformemente na parte superior da barra e uma carga está distribuída uniformemente na parte inferior. Determine (a) o módulo e (b) a orientação (em relação ao semieixo positivo) do campo elétrico no ponto , situado no centro do semicírculo.
Passo 1
Fala aí, pessoal! 😉
Bem, para essa questão iremos utilizar o campo elétrico de um arco de circunfência carregada (tem essa fórmula e a dedução dela no início desse capítulo no livro), o campo elétrico no centro de um arco circular é:
Em que é a densidade linear de carga. Nessa questão, cada quarto de circunferência faz um campo elétrico, onde varia de a como vemos na imagem do enunciado, tem o módulo igual a:
Colocamos , pois os limites de integração variam de a , então a variação total deve ser igual a .
Veja só! 👀
Passo 2
Agora que achamos o módulo, vamos achar as direções dos campos elétricos. Vamos lembrar que o campo devido a carga negativa é convergente (aproximação) e devido a carga positiva é divergente (afastamento).
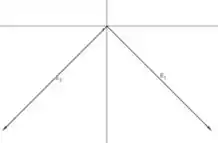
O ângulo que o campo devido ao arco de cima (positivo) faz com o semieixo positivo é , enquanto o ângulo do vetor campo elétrico devido ao arco debaixo (negativo) em relação ao semieixo é de . Aí você me pergunta: mas e as outras componentes que apontam para as outras direções?
Bom, como temos simetria entre o arco positivo em cima e o arco negativo embaixo, muitas componentes se cancelam até restarem apenas essas duas.
Os vetores ficam assim:
Bora lá! 😉
Passo 3
Item (a)
O módulo do campo total será dado apenas por uma componente em y, já que as componentes em x se cancelam devido aos vetores e serem iguais em módulo e terem componentes em x iguais ( se cancelam):
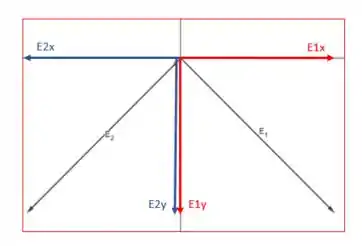
Então basta decompor os vetores no eixo (, isto é, multiplicar por que é o ângulo que eles fazem com o semieixo y negativo:
Substituindo os valores do enunciado, temos
Tranquilo até aqui? 😉
Passo 4
Item (b)
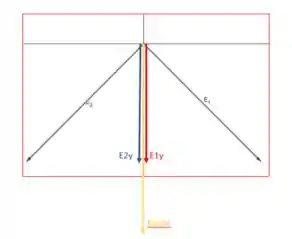
Por simétrico, como vimos anteriormente, o campo faz um ângulo de com o semieixo positivo.
E aí! entendeu tudo? Responde Aí! 😉
Resposta
-90° com o semieixo x positivo.