Campo Magnético Gerado por um Fio
Teoria
Fala aí! Bora aprender a calcular o Campo magnético Gerado por um Fio?
Então vamos com tudo! Vamos considerar um ponto
-Hãm??! 😵💫
Se liga no esquema:
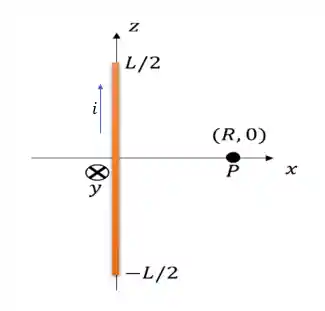
O movimento da corrente
O módulo do campo magnético gerado por um fio é dado por:
Onde
Talvez você até já esteja familiarizado com essa fórmula, lá do ensino médio! Perfeito, tranquilinho, sucesso! Não é?!
-Não!
Não é exatamente essa equação que vamos usar, infelizmente! 🥲
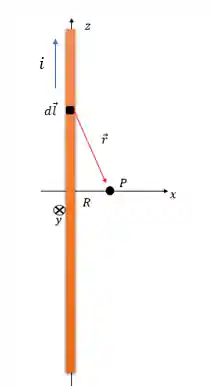
Vou te explicar o porquê, se liga nessa imagem:
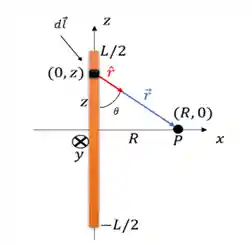
Precisamos conseguir calcular o campo magnético considerando qualquer lugar do fio! Nesse caso precisamos incluir o cálculo dessa distância
Essa é a Lei de Biot-Savart para correntes!
Mas, putz, integral de vetor? 🥲
Muita calma nessa hora! Existe um jeito da gente integrar só o módulo se soubermos a direção do campo!
Na imagem acima já temos esse dado, mas você também pode descobrir essa informação usando a regra da mão direita! Para isso coloca a sua mão direita com o polegar apontando pro sentido da corrente e com a mão envolvendo o fio.
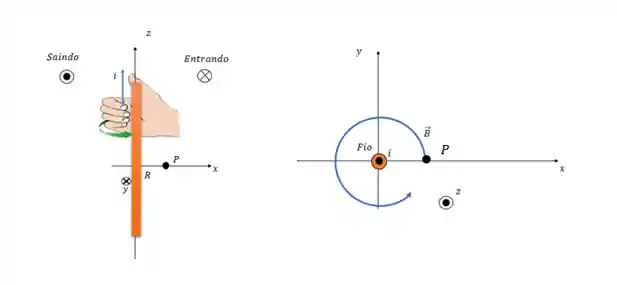
- Clique aqui para aprender mais sobre: Regra da Mão Direita
Podemos ver que no lado do ponto
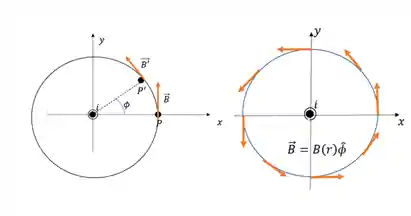
Usando o teorema de Pitágoras e fazendo algumas manipulações, ficamos com:
Esse
Campo Magnético Gerado por um Fio infinito
Como assim Fio Infinito?! 😱
Calma! Dizemos que um fio é infinito quando o seu comprimento
Comparado ao comprimento
Então a fórmula do campo magnético para o fio infinito fica:
Agora confere esse vídeo sobre campo magnético gerado por um fio que eu separei especialmente pra você:
Bora praticar com exercícios?!
Campo Magnético Gerado por um Fio infinito
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 253-9.
Na figura abaixo, dois fios retilíneos longos são perpendiculares ao plano do papel e estão separados por uma distância .
O fio 1 conduz uma corrente de para dentro do papel. Determine o módulo e o sentido (para dentro ou para fora do papel) da corrente no fio 2 para que o campo magnético seja zero no ponto , situado a uma distância do fio 2.
Passo 1
O campo magnético gerado por um fio longo é dado por:
Assim, para que o campo magnético seja nulo em , é necessário que:
Simplificando essa expressão, a corrente no fio 2 será:
Onde:
Finalmente:
Passo 2
A corrente no Fio 1 gera, em , um campo magnético para a esquerda. Para que os campos se anulem, o Fio 2 deve gerar um campo magnético para a direita em .
Através da regra da mão direita, isso só vai ser possível se o sentido da corrente for para fora do papel, conforme a figura abaixo:
Resposta
O sentido da corrente do Fio 2 está para fora do papel.
Exercício Resolvido #2
UFRJ – Prova Final – 2014.1 – Múltipla Escolha nº7.
Dois fios retilíneos muito longos, paralelos, a uma distância de entre si, transportam, cada um, uma corrente elétrica estacionária de . O módulo da força magnética por unidade de comprimento que cada um exerce sobre o outro é:
.
.
.
.
.
Passo 1
A força magnética sobre um fio retilíneo é dada por:
Onde o campo magnético gerado pelo fio 1 é dado por:
Substituindo na expressão da força magnética, teremos:
Assim, a força por unidade de comprimento será:
Sabendo que e , teremos:
A resposta certa é a letra .
Resposta
.
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 254-16.
A figura abaixo mostra, em seção reta, quatro fios finos paralelos, retilíneos e muito compridos, que conduzem corrente iguais nos sentidos indicados.
Inicialmente, os quatro fios estão a uma distância da origem do sistema de coordenadas onde criam um campo magnético total .
Para que valor de o fio 1 deve ser deslocado sobre o eixo para que o campo sofra uma rotação de no sentido anti-horário?
Com o fio 1 na nova posição, para que valor de o fio 3 deve ser deslocado sobre o eixo para que o campo volta à orientação inicial?
Passo 1
O primeiro passo é ver onde está o campo magnético original. Como as correntes são iguais e as distâncias iniciais também são, os módulos dos campos magnéticos de cada fio também serão iguais.
Logo, usando a regra da mão direita, podemos determinar para onde estão esses campos:
Assim, o campo magnético resultante será:
Passo 2
Para que valor de o fio 1 deve ser deslocado sobre o eixo para que o campo sofra uma rotação de no sentido anti-horário?
Antes de começar, vamos defini como sendo a componente em do campo magnético total e como sendo a componente em do campo magnético total. Onde:
Nesse caso, como não vamos mexer com os fio 2 e 4, será dado por:
Além disso, como não vamos mexer com o fio 3:
Continuando...
Agora, para que haja uma rotação de no sentido anti-horário, é necessário que:
Vamos reorganizando esse cara até acharmos o que estamos procurando:
Substituindo as expressões dos campos magnéticos, teremos:
Simplificando os termos:
Onde , finalmente:
SE LIGA!!!!!!!
Aqui tem uma pegadinha... o problema pergunta para que valor de o fio 1 deve ser deslocado. Assim, como ele deve ficar a da origem, ele deve ser deslocado para a posição:
Passo 3
Com o fio 1 na nova posição, para que valor de o fio 3 deve ser deslocado sobre o eixo para que o campo volta à orientação inicial?
Para que volte à orientação inicial, o campo magnético deve cancelar o campo magnético . Isso só vai acontecer se os dois estiverem à mesma distância da origem.
Assim, o fio 3 deve ser deslocado para a posição:
Resposta
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 257-36.
Na figura abaixo, quatro fios retilíneos longos são perpendiculares ao papel, e suas seções retas formam um quadrado de lado .
Todos os fios conduzem correntes de para fora do papel. Em termos dos vetores unitários, qual é a força magnética por metro de fio que age sobre o fio 1?
Passo 1
Ok, vamos começar definindo os as forças que agem sobre o fio 1.
Como todas as correntes são iguais, os módulos de cada força serão:
Passo 2
Beleza, agora que já definimos os módulos, precisamos olhar para os vetores. Como todos os fios possuem correntes paralelas, todas as forças serão atrativas, logo:
Assim, as forças serão dadas por:
Passo 3
Assim, a força resultante sobre o fio 1 será:
Por fim, a força resultante por unidade de comprimento será:
Onde:
Finalmente:
Resposta
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 257-37.
Na figura abaixo cinco fios paralelos longos no plano estão separados por uma distância .
As correntes para dentro do papel são , , e , a corrente para fora do papel é Qual é o módulo da força por unidade de comprimento que age sobre o fio 3?
Passo 1
Beleza, o primeiro passo aqui é calcular o módulo de cada uma das forças em 3:
Passo 2
Beleza, o primeiro passo aqui é colocar graficamente onde estão cada uma dessas correntes para nos orientarmos... de acordo com o enunciado, o esquema é esse aqui:
Lembrando que, quando as correntes são paralelas os fios se atraem e quando são antiparalelas, os fios se repelem.
Dessa forma:
Passo 3
A força resultante sobre o fio 3 será:
A força resultante por unidade de comprimento será:
Vou só dar uma arrumada pra facilitar os cálculos, de boa?
Onde:
Jogando esses valores na expressão acima, teremos:
Resposta
Exercício Resolvido #6
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 28.28, pp. 273.
Três fios paralelos e muito longos conduzem correntes de módulo igual a , com os sentidos indicados na Figura abaixo. Sabendo que a distância entre dois fios adjacentes é igual a , calcule o módulo, a direção e o sentido da força magnética resultante por unidade de comprimento sobre cada fio.
Passo 1
Para gente calcular a força resultante em cada um dos fios acima, precisamos saber qual é o campo magnético resultante sobre cada um deles devido a todos os outros.
No primeiro fio de cima, o módulo vetor campo magnético resultante será
Esse campo magnético está entrando no plano da página, de modo que o vetor é
A força que age nesse fio é
Portanto, a força por unidade de comprimento é dada por
Passo 2
Já no fio do meio, o campo resultante será nulo, pois as correntes dos fios de cima e de baixo produzem um campo que tem mesmo módulo, mesma direção, mas sentidos contrários e, por isso, se cancelam.
Portanto, a força por unidade de comprimento que age no fio do meio é NULA.
Passo 3
Por último, o módulo vetor campo magnético resultante no último fio de baixo será
Esse campo magnético está saindo do plano da página, de modo que o vetor é
A força que age nesse fio é
Assim, temos que a força por unidade de comprimento no último fio de baixo é dada por
Resposta
Primeiro fio de cima:
Fio do meio:
Fio de baixo:
Exercício Resolvido #7
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 28.60, pp. 276.
A Figura abaixo representa o plano que corta perpendicularmente dois fios longos (infinitos) e paralelos que conduzem uma corrente , de mesmo módulo, porém de sentidos contrários.
- Copie o diagrama e desenhe os vetores para mostrar que o campo magnético de cada fio e campo resultante no ponto .
- Deduza uma expressão para o módulo do campo em qualquer ponto do eixo em termos da coordenada do ponto. Qual é a direção e o sentido de ?
- Para qual valor de o módulo de atinge seu valor máximo?
- Qual é o módulo de quando ?
Passo 1
a) Na Figura abaixo, o fio de cima chamamos de e o debaixo de . O campo produzido por eles, e , respectivamente, são perpendiculares às linhas tracejadas de comprimento .
O campo magnético resultante no ponto é dado por
sendo que tem módulo
Passo 2
b) Da Figura acima, vemos que o vetor campo magnético resultante estará ao longo do eixo e terá módulo dado por
em que utilizamos, a partir da Figura acima, que
Passo 3
c) Se derivamos com relação a o módulo do vetor campo magnético resultante, chegamos a
Portanto, o campo magnético resultante é máximo em .
Passo 4
d) Se , então o campo magnético resultante é
Resposta
- Desenho da Figura ;
- é máximo em
Exercício Resolvido #8
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 28.63, pp. 276.
Dois fios longos e paralelos estão suspensos por meio de cordas de de comprimento, presas a um eixo comum, como mostra a Figura abaixo. Os fios possuem massa por unidade de comprimento igual a e conduzem correntes de mesmo módulo, porém de sentidos contrários. Qual é a corrente em cada fio, sabendo que as cordas de sustentação formam um ângulo de com a vertical?
Passo 1
Para matar esse exercício, imagina que você está vendo a Figura acima de perfil, como na Figura abaixo, de maneira que a corrente no fio da esquerda está entrando no plano da página e a da direita saindo da página.
A corrente da esquerda produz um campo magnético no fio da direita que aponta para baixo. Isso você pode verificar usando a regra da mão direita para corrente. Um campo de mesma intensidade é produzido pela corrente da direita no fio da esquerda e aponta também para baixo. Esses campos têm uma intensidade que é dada por
Como é perpendicular às correntes em ambos os fios, então a força magnética que age nos dois fios tem mesma direção, mesma intensidade, porém sentidos diferentes, como está mostrado na Figura. Por isso, os fios nessa situação de afastam um do outro. A intensidade dessa força é
em que é o comprimento dos fios percorridos pelas correntes e é a distância entre os dois fios.
Passo 2
Como os fios estão em equilíbrio com as cordas de comprimento fazendo um ângulo com a vertical, vamos escrever as componentes das forças em cada um dos eixos. Fazendo isso, vamos encontrar
Se a gente divide a primeira equação acima pela segunda, obtemos o seguinte
Colocando aqui dentro a expressão que encontramos lá no Passo 1, temos
Bom, nessa fórmula, ainda não conhecemos o valor de nem de (não confunda esse comprimento com , que o comprimento das cordas que estão segurando os fios!!), que são quantidades não fornecidas pelo enunciado. Vamos continuar...
Passo 3
Para completar, vamos deixar a expressão para a corrente acima em termos apenas das quantidades fornecidas pelo enunciado.
Para isso, o exercício diz que a massa dos fios percorridos pela corrente pode ser escrita como
em que é conhecido, mas não sabemos o valor de , mas isso não vai ser um problema, como você vai ver logo logo! :-).
Continuando, da Figura acima, a gente tem também que
e aqui , comprimento das cordas, é conhecido. Colocando isso tudo junto lá na expressão para , chegamos no seguinte
que não depende do comprimento dos fios percorridos pela corrente . Tranquilo?
Colocando os valores dados no enunciado dentro dessa expressão, com a ajuda da nossa amiga calculadora, você vai encontrar que o valor da corrente é
Resposta
Exercício Resolvido #9
Site do Prof. A. F. Guimarães, lista 09 de Física 3, Questão 03
Quatro longos fios são dispostos ortogonalmente ao plano da página, como mostra a figura abaixo, sendo cada um deles percorrido, no sentido indicado, por uma corrente . Determine o vetor resultante no centro do quadrado.
Passo 1
Primeiramente, quando ele diz “longos fios”, ele quer dizer infinito. Agora, temos que lembrar que o módulo do campo magnético produzido por uma corrente transportada em um fio condutor infinito é:
Sendo R, a distância do ponto P até o fio.
Passo 2
Feito isso, nós vamos utilizar a regra da mão direita (como em todos os exercícios haha) em cada um dos fios.
Sejam as correntes 1, 2, 3 e 4, conforme a figura abaixo, nósteremos os respectivos campos magnéticos , . Em todos os outros pontos a intereção das 4 correntes irá gerar um campo magnético nulo.
Lembrando que isso só ocorre pois todas as correntes possuem uma corrente de mesma intensidade, .
Passo 3
Por questões de simetria, todas as componentes horizontais irão se cancelar, sobrando apenas a componente vertical.
Temos que o módulo dos campos é dado por:
E como temos a soma dos quatro campos vamos ter que o campo magnético resultante é dado por:
E sabemos que o valor de é dado pela metade da diagonal do quadrado, ou seja:
Substituindo:
Agora só falta calcular a componente vertical do nosso campo magnético resultante:
Por se tratar de um quadrado, sabemos que o ângulo (em verde na figura) é de 45º.
Sendo assim, temos: