Momento Magnético
Produzido por Bruno SoaresTeoria
Fala aí! A ideia de hoje é entender o que é o momento magnético e o que fazer quando nos depararmos com esse cara em algumas situações.
Antes de qualquer coisa, vou deixar aqui embaixo alguns links que tratam de conhecimentos prévios que você precisa estar dominando antes de darmos sequência, beleza?
⭐ Veja também ⭐
Momento Dipolo Magnético
O momento magnético dipolar é um vetor que representa a intensidade da fonte magnética.
Para descobrirmos o sentido desse vetor, usamos a regra da mão direita no sentido da corrente. (Seu polegar aponta no sentido do momento dipolo magnético e os demais dedos curvam-se no sentido da corrente)
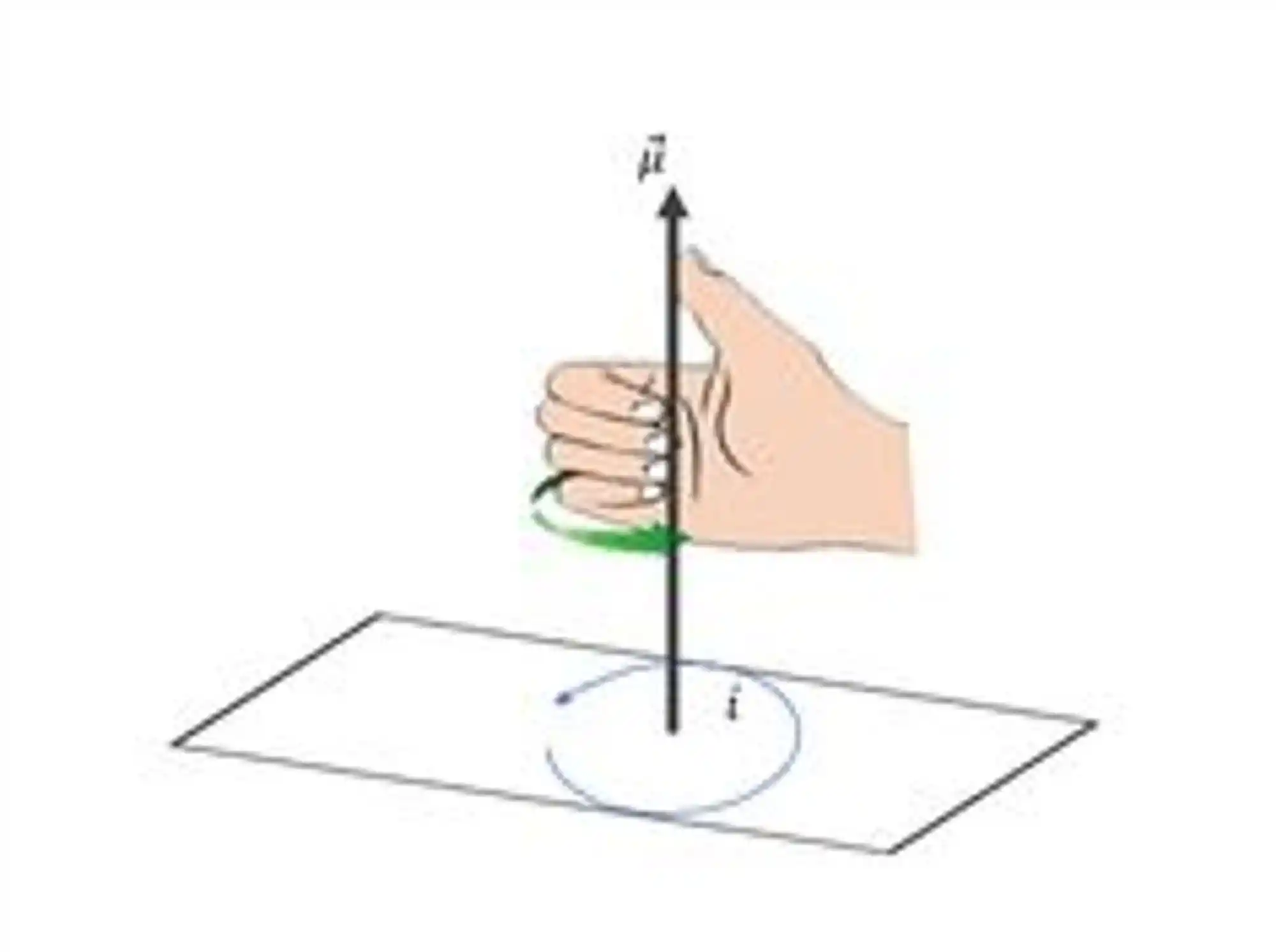
O momento de dipolo magnético
👉
👉
O vetor
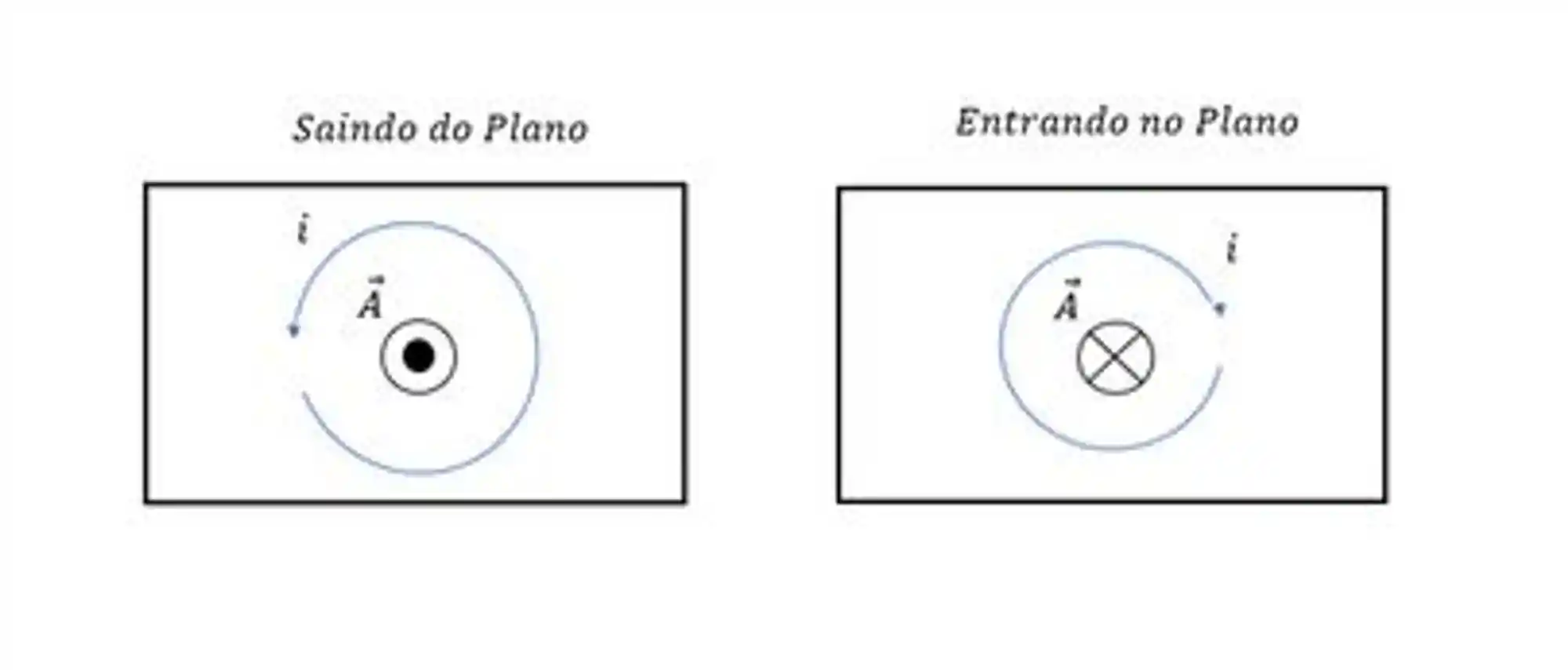
Momento Dipolo Magnético de uma Bobina
Uma bobina se comporta como uma espira enrolada várias vezes.
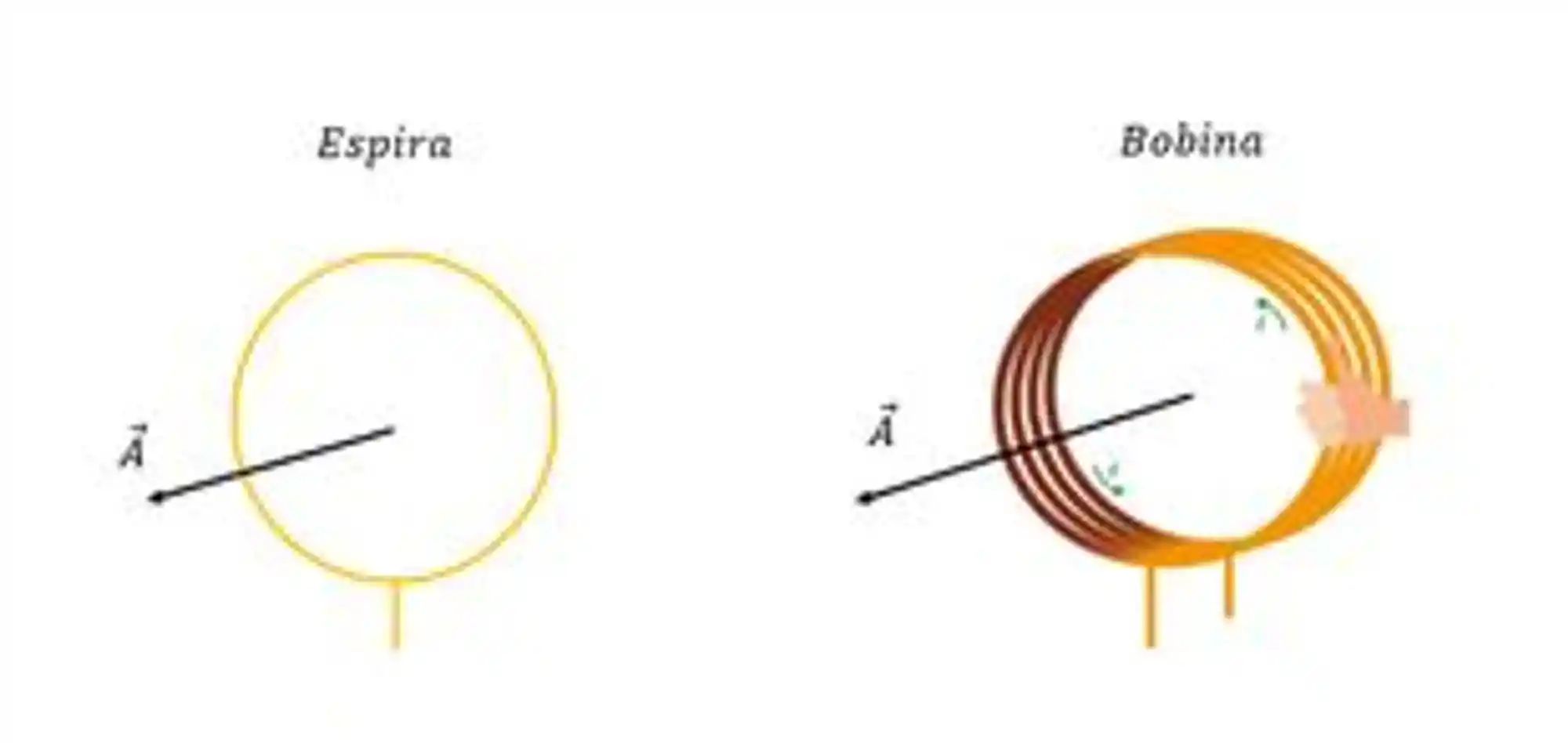
Quer dizer que podemos aproveitar a equação anterior. Com uma pequena modificação, chegamos em uma expressão para uma espira enrolada n vezes:
Torque Magnético em uma Espira
Na presença de um campo magnético, uma espira sofre ação de um torque magnético (
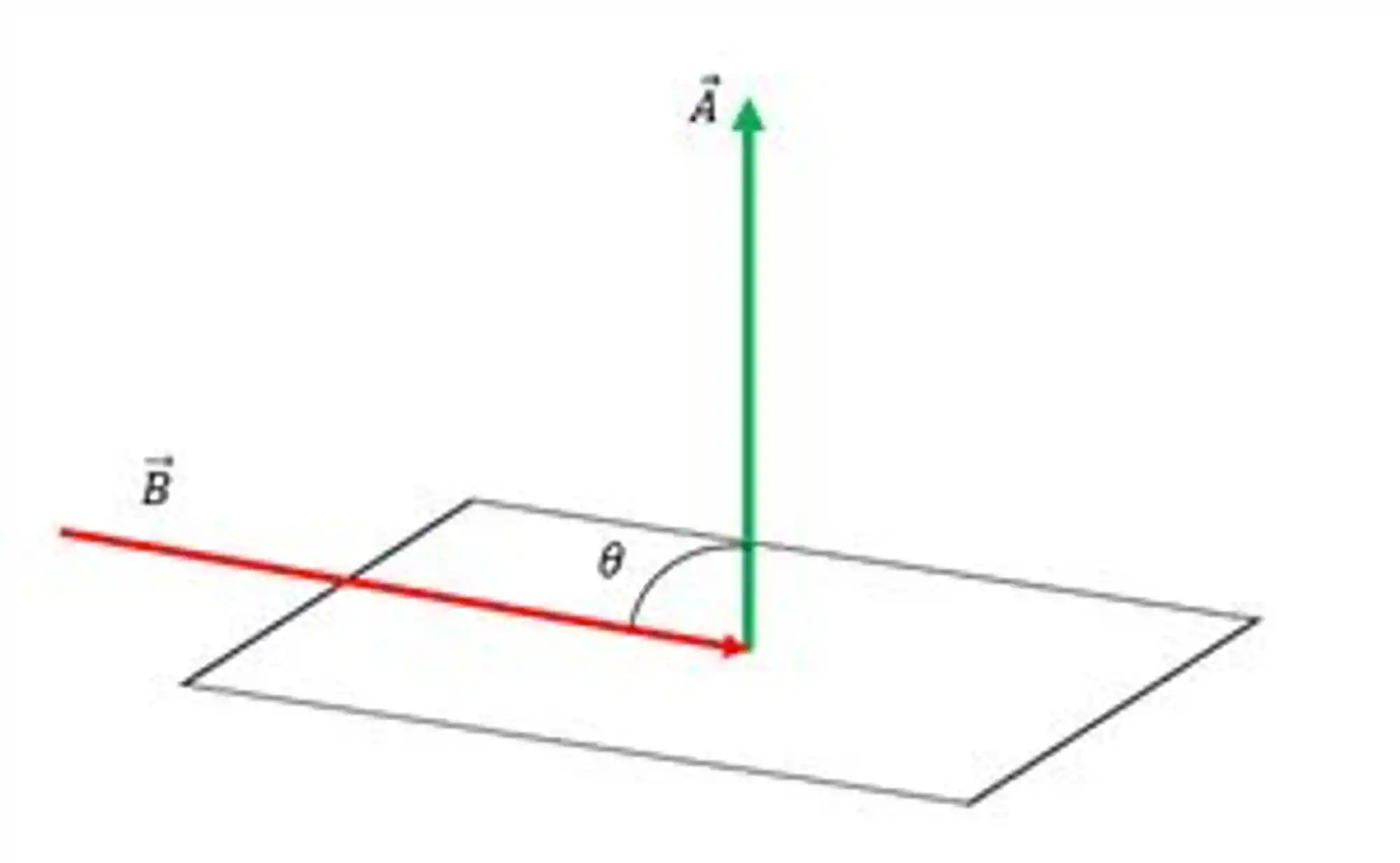
Mas não se assuste com aquele produto vetorial! Ele pode ser substituído:
O que importa mesmo para o torque é o ângulo entre o vetor área e o campo magnético! Ele possui valor máximo quando
E mínimo quando
Energia Potencial Magnética
Na presença de um campo magnético, um dipolo possui uma energia potencial magnética (U).
Essa energia é dada pelo produto escalar:
E esse produto escalar também pode ser reescrito da seguinte forma:
Trabalho Magnético sobre uma Espira
Se um agente externo faz o dipolo magnético girar de uma orientação inicial para uma orientação final, e se o dipolo permanece estacionário, o trabalho
Belezinha? Bora praticar com alguns exercícios resolvidos pra ficarmos craques nisso aí.
Momento Dipolo Magnético de uma Bobina
Torque Magnético em uma Espira
Energia Potencial Magnética
Trabalho Magnético sobre uma Espira
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 229-56.
O módulo de momento dipolar magnético da Terra é . Suponha que esse momento é produzido por cargas que circulam na parte externa do núcleo da Terra. Se o raio da trajetória dessas cargas é , calcule a corrente associada.
Passo 1
O momento dipolar magnético é dado por:
Como as cargas estão circulando o núcleo da Terra, a área compreendida pela trajetória delas é . Logo:
Onde .
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 229-59.
Duas espiras circulares concêntricas, de raios e , estão situadas no plano . Ambas são percorridas por uma corrente no sentido horário, conforme a figura abaixo.
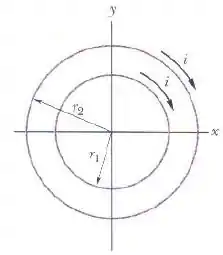
Determine o módulo do momento dipolar magnético do sistema.
Repita o cálculo supondo que a corrente da espira menor mudou de sentido.
Passo 1
Determine o módulo do momento dipolar magnético do sistema.
Nesses casos, o momento dipolar do sistema será a soma de todos os momentos dipolares, logo:
Como as duas correntes estão no mesmo sentido, os momentos dipolares terão o mesmo sinal, logo:
Onde:
Portanto:
Passo 2
Repita o cálculo supondo que a corrente da espira menor mudou de sentido.
A lógica aqui é a mesma, a diferença é que, como as correntes estão em sentidos contrários, os momentos irão ter sinais diferentes, logo:
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #3
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 230-61.
Uma espira circular com de raio é percorrida por uma corrente de .
Um vetor de comprimento unitário, paralelo ao momento dipolar da espira é dado por . Se a espira é submetida a um campo magnético uniforme dado por
Determine o torque sobre a espira (em termos dos vetores unitários) e a energia potencial magnética da espira.
Passo 1
Determine o torque sobre a espira (em termos dos vetores unitários);
O torque magnético sobre a espira é dado por:
Vamos começar calculando o momento dipolar magnético, que é dado por:
Onde e .
Assim, o vetor momento dipolar magnético será dado por:
Onde é o vetor unitário na direção e sentido de , logo:
Passo 2
Assim, o torque magnético será:
Passo 3
A energia potencial magnética é dada por:
Finalmente:
Resposta
Exercício Resolvido #4
UFRJ – Prova 2 – 2012.2 – Múltipla escolha nº10.
Uma bússola encontra-se acima de um fio retilíneo, muito longo, percorrido por uma corrente elétrica estacionária de intensidade . Na sua posição de equilíbrio estável, quais são o sentido do vetor momento de dipolo magnético da bússola e a sua energia potencial , supondo que esta última é zero quando .
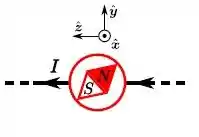
- e
- e
- e
- e
- e
- e
Passo 1
O sentido do momento de dipolo de um imã é do Sul pro Norte. O torque é dado por:
Sabemos que o campo gira em torno do fio. Utilizando a regra da mão direita, coloque o polegar no sentido da corrente que os outros dedos dão o sentido do campo.
Como a bússola está acima, podemos visualizar o campo vendo a figura de lado:
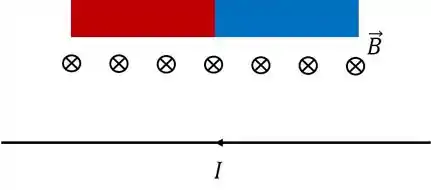
Passo 2
Logo, o sentido do campo é . O equilíbrio é atingido quando não há torque:
Que é quando o campo e o momento de dipolos são paralelos.
Passo 3
O equilíbrio é estável quando a energia potencial é mínima. A energia potencial tem fórmula:
Que equivale a:
Este valor é mínimo para :
Portanto é quando o e o apontam no mesmo sentido, ao invés de sentidos opostos. Por consequência, o sentido de é e o valor da energia é , conforme calculado.
Resposta
Letra a
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 229-52.
Um elétron se move em um círculo de raio com uma velocidade de .
Trate a trajetória circular como uma espira de corrente igual à razão entre a carga do elétron e o período do movimento.
Se a trajetória do elétron está em uma região onde existe um campo magnético uniforme de módulo , qual é o maior valor possível do módulo do torque aplicado pelo campo à espira?
Passo 1
Bom, sabendo que o torque sobre uma espira é dado por:
O maior valor possível do módulo do torque vai ocorrer quando e forem perpendiculares... já que poderíamos reescrever a fórmula do torque dessa forma:
Onde é o ângulo entre e .
Assim, se eles forem perpendiculares, e .
Então vamos usar essa fórmula aqui embaixo pra calcular o maior torque possível.
Onde . Logo:
Passo 2
Beleza, rapaziada... se o elétron percorre a trajetória circular, podemos considerar a nossa espira como um círculo, assim:
Passo 3
Sobre a corrente, o enunciado já deu essa de bandeja pra a gente quando diz “corrente igual à razão entre a carga do elétron e o período da trajetória”.
Pra calcular o período da trajetória, podemos fazer o seguinte:
Assim:
Vamos jogar isso na fórmula do torque e ver no que vai dar.
Passo 4
Onde:
;
;
;
;
Vambora!
Resposta
Exercício Resolvido #6
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 230-65.
A bobina da figura conduz uma corrente no sentido indicado, é paralela ao plano , tem espiras, tem uma área de e está submetida a um campo magnético uniforme .
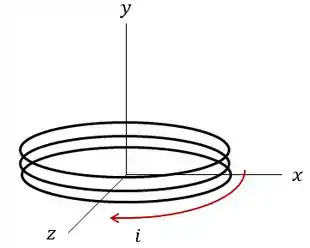
Determine:
- A energia potencial magnética do sistema bobina-campo magnético;
- O torque magnético (na notação de vetores unitários) a que está sujeita a bobina;
Passo 1
- A energia potencial magnética do sistema bobina-campo magnético;
- O torque magnético (na notação de vetores unitários) a que está sujeita a bobina;
A energia potencial magnética é dada por:
Pra esse caso, com uma bobina com espiras:
Onde:
;
;
;
Logo:
Passo 2
Agora ficou fácil! ;)
Onde .
Passo 3
O torque magnético sobre uma espira é dado por:
Onde:
;
;
Logo:
Resposta
- ;
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 228-47.
A figura abaixo mostra uma bobina retangular de cobre, de 20 espiras, com de altura e de largura.
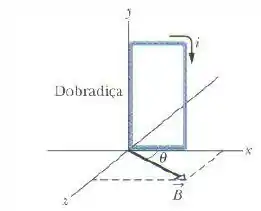
A bobina conduz uma corrente de e dispões de uma dobradiça em um dos lados verticais. Ela está montada no plano , fazendo um ângulo de com a direção de um campo magnético uniforme de módulo .
Em termos dos vetores unitários, qual é o torque que o campo exerce sobre a bobina em relação à dobradiça?
Passo 1
O torque magnético sobre uma espira é dado por:
Então precisamos encontrar cada vetor.
O momento dipolo magnético é dado por:
Onde:
Além disso, utilizando a regra da mão direita, a partir da corrente elétrica, vemos que o momento dipolo magnético está no sentido .
Logo:
Passo 2
O campo magnético vale e faz um ângulo de com o eixo , logo, o vetor campo magnético será dado por:
Passo 3
Agora sim, o torque magnético será dado por:
Resposta
Exercício Resolvido #8
USP – Física III – Prova 2 – 2011 – Questão 3
Um fio condutor, curvado na forma de um semicírculo de raio , forma um circuito fechado e é percorrido por uma corrente . O circuito está no plano e um campo magnético uniforme está aplicado paralelamente ao eixo , com é visto na figura.
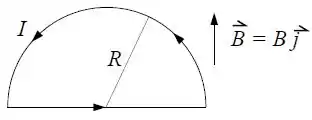
Determine a força magnética total (vetor) sobre a parte retilínea do condutor.
Determine a força magnética total (vetor) sobre a parte curva do condutor.
Determine o vetor torque exercido por sobre o circuito.
Passo 1
Determine a força magnética total (vetor) sobre a parte retilínea do condutor.
Por definição, a força magnética sobre uma espira é dada por:
Onde está sempre na mesma direção e sentido da corrente.
No caso de um condutor retilíneo, podemos dar uma simplificada nesse cara que, agora, terá essa cara:
Onde, novamente, tem a direção e sentido da corrente.
Passo 2
Nesse problema, olhando a figura, podemos concluir que:
Portanto:
Passo 3
Determine a força magnética total (vetor) sobre a parte curva do condutor.
Aqui, como se trata se um condutor curvado, vamos usar essa expressão para a força magnética:
Beleza, vamos dar uma olhada no vetor nesse caso:
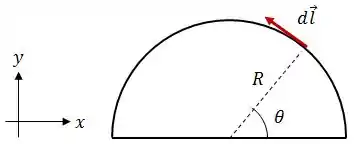
Daqui podemos decompor o vetor em componentes nas direções e .
Substituindo isso na expressão de , teremos:
Agora é só organizar esse cara e fazer as contas:
Passo 4
Determine o vetor torque exercido por sobre o circuito.
Por definição, o torque sobre uma espira é dada por:
Onde é o momento dipolar elétrico, definidor por:
Onde é o vetor cujo módulo é igual à área que do circuito, direção perpendicular ao plano do circuito e sentido dado pela regra da mão direita.
Como a corrente flui no sentido anti-horário, pela regra da mão direita, teremos:
Logo:
E, finalmente, o torque será dado por:
Resposta