Circuitos RLC
Produzido por Bruno SoaresTeoria
Um circuito RLC é composto por um resistor
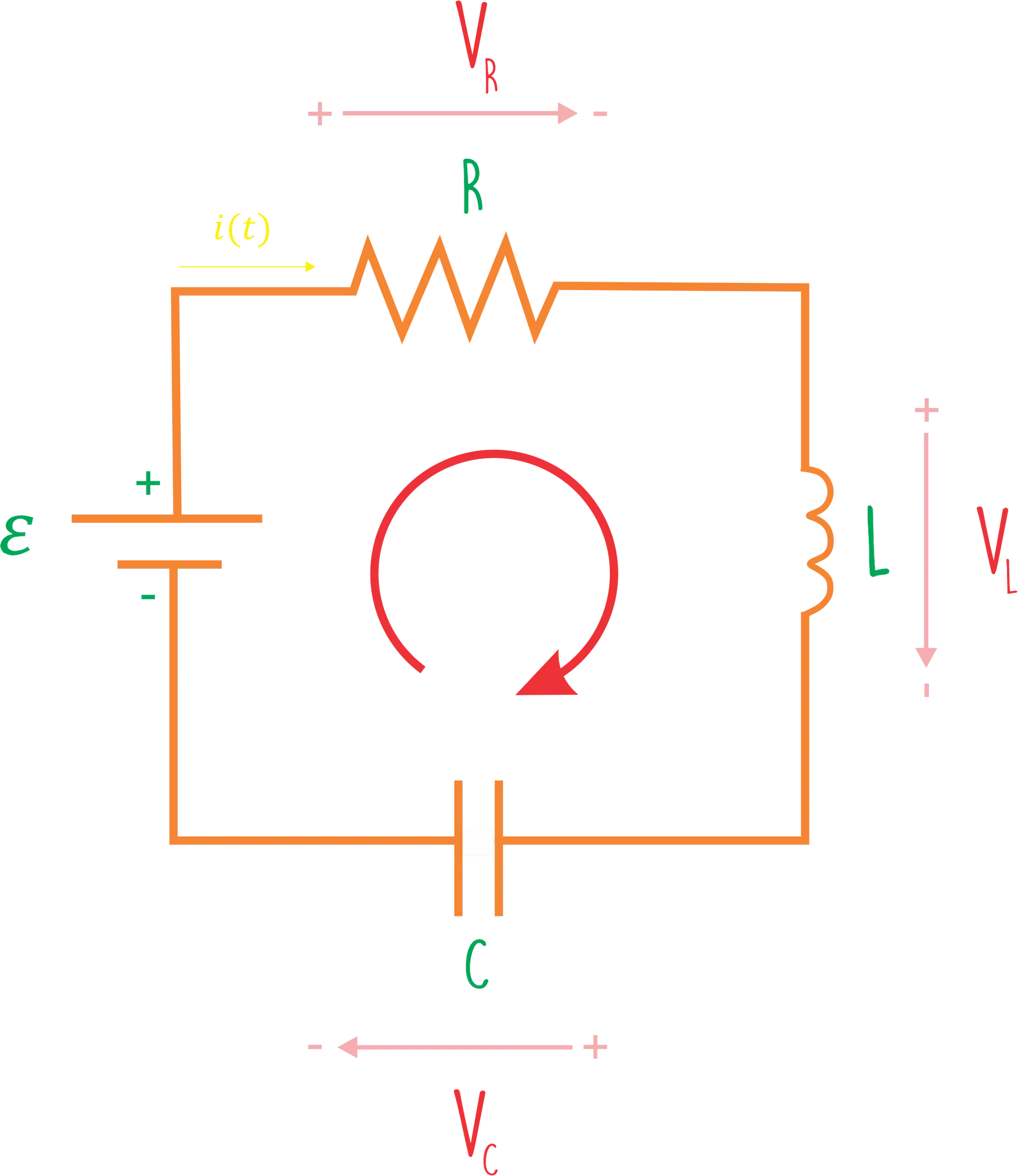
Dizemos que o circuito RLC é um circuito de segunda ordem, isso porque suas equações são descritas por EDOs de 2ª ordem! E hoje a gente vai aprender tudo sobre esse circuito pra arrasar na prova! 😍
📢 Clique para ver mais:
Circuito LC
Antes da gente chegar ao que interessa, vamos dar uma olhadinha em como funciona o circuito LC, que tudo vai ficar mais fácil depois! O circuito LC é composto por um indutor e por um capacitor, ele tem essa carinha aqui:
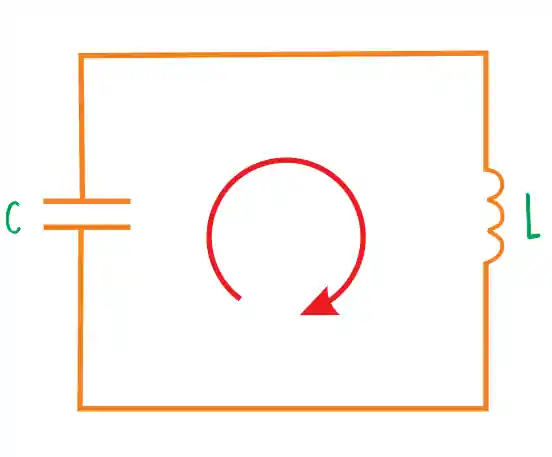
Só pra relembrar, o capacitor armazena energia em seu campo elétrico e o indutor é responsável por induzir a
Tendo em vista o comportamento da corrente, fazemos um análogo entre o circuito LC e o movimento oscilatório, vamos então começar analisando as energias envolvidas:
- A energia armazenada no campo elétrico do capacitor é
- A energia armazenada no campo elétrico do indutor é é
Analogamente ao movimento oscilatório, a soma dessas energias é sempre constante:
Onde
Podemos substituir
Essa é uma equação diferencial de segunda ordem, que possui a seguinte solução:
Derivando, podemos determinar a corrente:
Daqui em diante temos uma corrente oscilatória conhecida como corrente alternada. Dessa equação, vemos que a amplitude de corrente é
Onde a frequência angular da oscilação,
Para indutor a voltagem é dada por:
Você também pode acessar esse conteúdo em vídeo:
Como funciona o Circuito RLC
O delta pode ser maior, igual ou menor que zero, então temos três possibilidades de solução.
Regime Supercrítico: Quando Δ>0
Nesse caso temos duas raízes reais, a equação auxiliar e a solução da carga são:
Sua corrente pode ser calculada por:
O gráfico para essa corrente fica da seguinte forma:

Regime Crítico: Quando Δ=0
Nesse caso temos apenas uma raiz real, dada por:
A solução pra carga e para a corrente serão:
O gráfico para essa corrente fica da seguinte forma:

Regime Subcrítico: Quando Δ<0
Nesse caso teremos duas raízes complexas para a equação auxiliar, dadas por:
A solução para a carga será igual a:
O gráfico para a corrente fica assim:
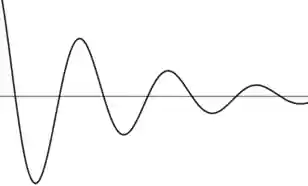
Tensão do Capacitor e do Indutor
Podemos também definir a tensão no capacitor e no indutor da seguinte forma:
Agora vamos praticar com exercícios?