Lei de Ampère em Solenóides e Toróides
Teoria
Já vimos como usar a lei de Ampère para calcular o campo magnético gerado por um fio com corrente . E se tivéssemos mais fios? Como seria?
Lei de Ampère para um plano infinito de fios
Vamos olhar para esse caso específico com dois fios e tentar calcular o campo magnético no ponto que está a mesma distância dos dois fios
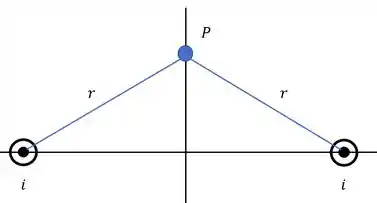
Já sabemos que o módulo do campo magnético gerado por cada um dos fios terá mesma magnitude e a direção de cada ponto será dada pela regra da mão direita.
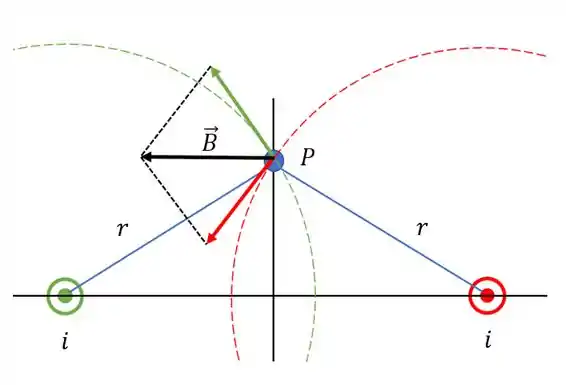
Ao somarmos as duas contribuições teremos somente um campo horizontal, já que as componentes verticais vão se anular!
Show! Mas o que isso tem de importante? Uma coisa que aparece muito é quando temos um plano com infinitos fios!
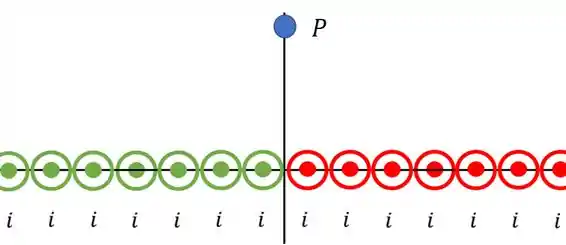
Para cada fio vermelho (à direita) haverá um fio verde (à esquerda), de forma que cada par de fios produzirá um campo magnético horizontal! Além disso esse campo também será uniforme!
A visualização fica mais ou menos assim
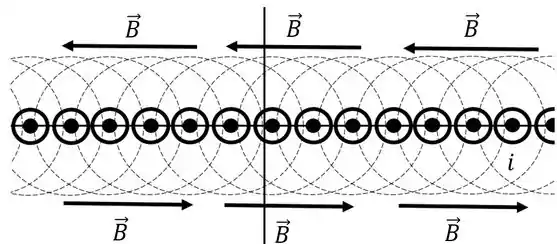
Pela regra da mão direita, acima do plano o campo magnético aponta para direita e abaixo do plano aponta para esquerda.
Beleza, agora podemos aplicar a lei de Ampère (lembra dela?) nesse problema!
Vamos escolher como curva amperiana um retângulo de altura e base , como na figura abaixo
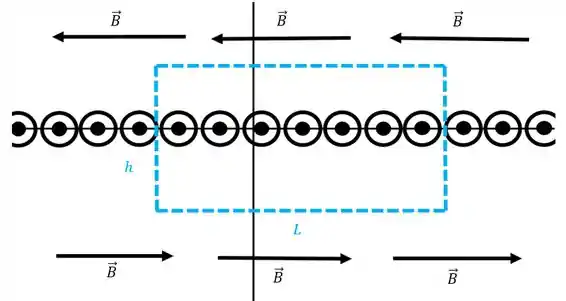
Pela lei de Ampère temos que
Como o campo é horizontal a integral de linha a esquerda só terá contribuição da base do retângulo.
Já a corrente , total passando por dentro da amperiana será o número de fios dentro dessa curva vezes a corrente em cada fio.
Supondo que nesse plano infinito há fios por comprimento, o total de fios dentro da amperiana será , de forma que
Juntando todas as informações temos
E aqui está o nosso campo \o/
Se liga, que vimos aqui o caso da corrente saindo do plano da folha! Quando a corrente estiver entrando a intensidade do campo é a mesma que vimos agora, mas a direção do campo muda (devido a regra da mão direita)
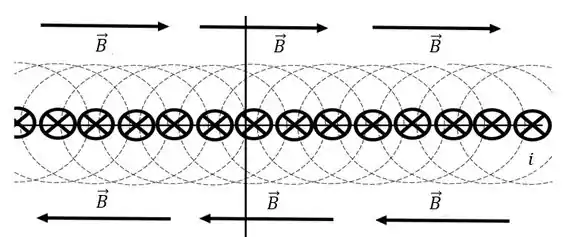
A boa agora é aplicar a Lei de Ampère para calcular o campo magnético no interior de solenóides e toróides. Cuidado para não confundir os nomes (eu, pelo menos, acho os dois meio parecidos). Então se liga!
Lei de Ampère em Solenóides
Um solenóide é uma bobina helicoidal formada por espiras circulares muito próximas.
No interior de um solenóide longo percorrido por uma corrente , em pontos distantes das extremidades (que é como costumam pedir nos problemas), o módulo do campo magnético é dado por:
Onde é o número de espiras por unidade de comprimento.
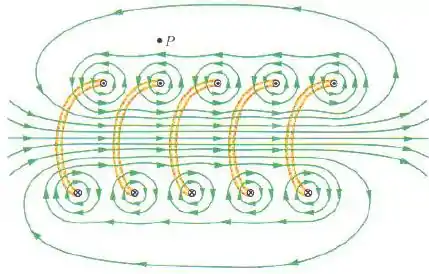
A representação das linhas de campo magnético em um solenoide é mostrada na figura abaixo por essas setas verdes.
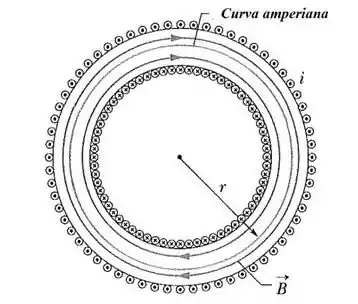
Lei de Ampère em Toróides
Um toróide pode ser descrito como um solenóide cilíndrico que foi encurvado até as extremidades se tocarem, formando assim um anel como o da figura abaixo.
Em um ponto no interior de um toróide o módulo do campo magnético é dado por:
Onde é o número total de espiras e é a distância entre o ponto e o centro do toróide.
Lei de Ampère em Solenóides
Lei de Ampère em Toróides
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 258-50
Um solenóide com de comprimento e de diâmetro conduz uma corrente de . O campo magnético no interior do solenóide é .
Determine o comprimento do fio que é feito o solenóide.
Passo 1
Pra começar, precisamos descobrir quantas espiras o solenóide possui.
O campo magnético no interior do solenóide é dado por:
Onde é o número de espiras por unidade de comprimento. Logo:
Substituindo na expressão do campo magnético, teremos:
Passo 2
O comprimento do fio necessário será vezes o comprimento da circunferência do solenóide, logo:
Onde:
Logo:
Resposta
Exercício Resolvido #2
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 258-51
Um toróide de seção reta quadrada, com de lado e um raio interno de tem espiras e conduz uma corrente de .
Determine o campo magnético no interior do toróide a uma distância do centro igual ao raio interno; a uma distância do centro igual ao raio externo.
Passo 1
Determine o campo magnético no interior do toróide a uma distância do centro igual ao raio interno;
O campo magnético no interior do toróide é dado por:
Onde:
Logo:
Passo 2
Determine o campo magnético no interior do toróide a uma distância do centro igual ao raio externo.
O raio externo será:
Onde é a medida do lado do quadrado, logo:
Beleza, partiu calcular o campo magnético:
Onde:
Logo:
Resposta
Exercício Resolvido #3
UFRJ – Física III – Prova Final – 2014.1 – Múltipla Escolha nº2.
Cada um de dois longos solenoides coaxiais é percorrido por uma corrente elétrica estacionária, de mesma intensidade , porém com sentidos contrários. Ambos os solenoide têm o mesmo comprimento , sendo que o interno possui raio e voltas, ao passo que o externo possui raio e voltas, sendo e .
Sendo a distância até o eixo comum dos solenoides, e considerando o campo magnético fora dos dois solenoides igual a , podemos expressar o campo magnético dentro do solenoide interno e entre os dois solenoides , respectivamente, como
; .
; .
; .
; .
; .
Passo 1
O campo magnético gerado por um solenoide é dado por:
Utilizando a regra da mão direita, escrevendo separadamente o campo magnético gerado por cada solenoide, teremos:
Agora vamos olhar cada região separadamente:
- :
- :
Nessa região, temos tanto o campo magnético gerado pelo solenoide externo, quanto pelo interno, logo:
Para essa região, consideraremos apenas o campo magnético gerado pelo solenoide externo. Isso acontece porque, na região fora de um solenoide, consideramos o campo magnético nulo, logo, como essa região está no exterior do solenoide interno, não vamos considerar o campo magnético gerado por ele.
Portanto:
A resposta certa é a letra .
Resposta
; .
Exercício Resolvido #4
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 28.45, pp. 274.
Um anel de madeira com diâmetro médio igual a é enrolado de modo compacto com espiras, formando um enrolamento toroidal. Determine o campo magnético em um ponto situado no centro da seção reta das espiras quando a corrente que passa no enrolamento é de .
Passo 1
Você viu aqui com a gente que, se temos um toróide com as dimensões da sua seção reta muito pequenas, o campo magnético produzido por um toróide com espiras conduzindo uma corrente é uniforme e dado por
sendo que é o raio médio do toróide. No caso desse exercício, o diâmetro do anel de madeira é e, portanto, . Substituindo os valores do enunciado mais o valor do raio médio dentro da expressão acima, temos
Esse é valor do campo magnético que atravessa cada uma das espiras do toróide e tem, aproximadamente, o mesmo valor dentro das espiras em todos os pontos, desde que a espessura do núcleo do toróide seja pequena comparada com o valor do raio , ou seja, que as dimensões da seção reta das espiras sejam muito pequenas. Essa é a uma justificativa muito importante, pois é só quando se tem essa geometria, ou aproximadamente isso, é que temos a expressão para o campo magnético que usamos neste exercício.
Resposta
Exercício Resolvido #5
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 28.44, pp. 274.
Um solenóide toroidal possui um raio interno e raio externo . O solenoide possui espiras e conduz uma corrente de . Qual é o módulo do campo magnético em um ponto cuja distância ao centro do toróide é:
- 12,0 cm?
- 16,0 cm?
- 20,0 cm?
Passo 1
Você viu aqui com a gente que o campo magnético produzido por um toróide com espiras pelas quais passa uma corrente é dado por
sendo que é o raio médio do toróide, como você pode visualizar na figura abaixo (deixa a sua imaginação fluir agora para enxergar espiras enroladas muuuuito juntas umas das outras...kkk Conseguiu? ):
O campo magnético produzido pelas correntes das espiras produz um campo magnético no interior do toróide, com sentido e direção indicados na figura acima. Se a espessura do núcleo do toróide for pequena comparada com o valor do raio médio , ou seja, , então o campo magnético é aproximadamente uniforme no interior do toróide, e tem o valor dado pela expressão acima, e os campos resultantes dentro, , e fora, , são aproximadamente NULOS. Geralmente, a gente fala só que é IGUAL A ZERO mesmo, sem dizer, na maioria dos problemas, a palavra “aproximadamente”, tranquilo?
Passo 2
a) No caso deste item, fica moleza, né? Dá uma olhada lá e repara que a distância que é considerada para este item é . Isso significa, como você consegue ver direto da figura agora, que o campo magnético nesse caso é
Passo 3
b) Já para , a gente acabou de ver que o campo, nas condições que mostrei pra você, tem praticamente o mesmo valor em todos os pontos do interior do toróide e você já viu e sabe agora que o campo lá dentro é
Tranquilo??
Passo 4
c) Agora com a figura que você tem aí em cima ficou molezinha demais resolver este item, né não? Dá uma olhada lá e veja que o campo magnético para , ou seja, fora do toróide é NULO!! Fechou, então! Checa lá na figura e veja que:
Resposta
Exercício Resolvido #6
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 28.43, pp. 274.
Um campo magnético de foi obtido no Francis Bitter National Magnetic Laboratory, do MIT. Determine a corrente necessária para atingir esse campo
- a de um fio longo e retilíneo;
- no centro de uma bobina circular de diâmetro igual a com espiras;
- próximo do centro de um solenóide com raio de , comprimento e espiras.
Passo 1
a) Aqui, a gente faz uma revisão muuuuuiiitoo rápida de uma das várias aplicações que a lei de Ampère tem. Você viu que o campo produzido a uma distância por um fio longo e retilíneo percorrido por uma corrente é dado por
e esse campo é sempre perpendicular ao fio e tem o mesmo valor para pontos à mesma distância do fio. Lembrou? \0/
Dessa expressão aí de cima, podemos isolar a corrente e escrever o seguinte
Passo 2
b) E se a gente usasse uma bobina e tentasse produzir o mesmo campo produzido pela corrente no fio retilíneo longo? Bom, para uma bobina com espiras percorridas por uma corrente , sabemos que campo que ela produz à uma distância de seu centro situado sobre o eixo de simetria da bobina é dado por
Se a gente precisa saber apenas o campo produzido pela bobina em seu centro, basta jogar nessa expressão e obter o campo
A corrente nesse caso fica então
Passo 3
c) Por último, o campo produzido por um solenóide é dado por
em que é o comprimento desse solenóide com espiras percorridas por uma corrente . Isolando nessa expressão, temos
Repara que a intensidade do campo magnético é obtido utilizando uma corrente bem menor quando se utiliza o solenóide com as dimensões citadas.
Resposta
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 9ª edição. Rio de Janeiro: LTC, 2012, pp 244
Um solenoide de 200 espiras com 25 cm de comprimento e 10 cm de diâmetro conduz uma corrente de 0,29 A. Calcule o módulo do campo magnético B no interior do solenoide.
Passo 1
Essa questão é muito simples, basta lembrarmos da fórmula da lei de ampére em solenoides:
Sendo que é a corrente passando pelo solenoide e é o número de espiras por unidade de comprimento.
Assim:
Sendo N o número de espiras do solenoide e l o comprimento do solenoide.
Passo 2
Agora que já temos a fórmula prontinha é só substituir os valores: