Exercícios de Lei de Ampère em Solenóides e Toróides - Lista de Exercícios Resolvida

Um solenóide com de comprimento e de diâmetro conduz uma corrente de . O campo magnético no interior do solenóide é .

Determine o comprimento do fio que é feito o solenóide.

Um anel de madeira com diâmetro médio igual a é enrolado de modo compacto com espiras, formando um enrolamento toroidal. Determine o campo magnético em um ponto situado no centro da seção reta das espiras quando a corrente que passa no enrolamento é de .

Um solenoide de 200 espiras com 25 cm de comprimento e 10 cm de diâmetro conduz uma corrente de 0,29 A. Calcule o módulo do campo magnético B no interior do solenoide.

Um campo magnético de foi obtido no Francis Bitter National Magnetic Laboratory, do MIT. Determine a corrente necessária para atingir esse campo

1. a de um fio longo e retilíneo;
2. no centro de uma bobina circular de diâmetro igual a com espiras;
3. próximo do centro de um solenóide com raio de , comprimento e espiras.

Um solenóide toroidal possui um raio interno e raio externo . O solenoide possui espiras e conduz uma corrente de . Qual é o módulo do campo magnético em um ponto cuja distância ao centro do toróide é:

1. 12,0 cm?
2. 16,0 cm?
3. 20,0 cm?

Um toróide de seção reta quadrada, com de lado e um raio interno de tem espiras e conduz uma corrente de .

Determine o campo magnético no interior do toróide a uma distância do centro igual ao raio interno; a uma distância do centro igual ao raio externo.

Cada um de dois longos solenoides coaxiais é percorrido por uma corrente elétrica estacionária, de mesma intensidade , porém com sentidos contrários. Ambos os solenoide têm o mesmo comprimento , sendo que o interno possui raio e voltas, ao passo que o externo possui raio e voltas, sendo e .

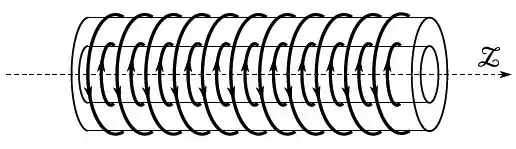
Sendo a distância até o eixo comum dos solenoides, e considerando o campo magnético fora dos dois solenoides igual a , podemos expressar o campo magnético dentro do solenoide interno e entre os dois solenoides , respectivamente, como

; .

; .

; .

; .

; .

Um solenoide toroidal, mostrado na figura e em corte transversal na figura , contém espiras e é percorrido por uma corrente . O núcleo do solenoide está preenchido por ar .

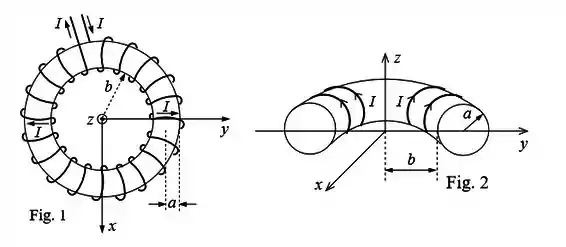
(a) Calcule o vetor campo magnético em coordenadas cartesianas isto é na forma ao longo do eixo para .

(b) Constrói-se um outro solenoide toroidal com as mesmas dimensões do solenoide da figura mas com um núcleo de aço inoxidável de permeabilidade . Passando a mesma corrente pelos dois solenoides, calcule a relação entre o número de espiras e no solenoide com núcleo de aço e com núcleo de ar, respectivamente, para produzir o mesmo campo magnético nos núcleos dos dois solenoides.

Um solenóide infinito transporta uma corrente cuja intensidade aumenta lentamente com o tempo. Sobre os campos produzidos por este sistema, é CORRETO afirmar que, dentro do solenóide:

(a) As linhas de campo elétrico induzido são circulares e estão em planos perpendiculares ao eixo do solenóide.

(b) As linhas de campo elétrico induzido são perpendiculares ao eixo do solenóide e apontam ao longo da direção radial.

(c) As linhas de campo magnético são circulares e estão em planos perpendiculares ao eixo do solenóide.

(d) As linhas de campo magnético são perpendiculares ao eixo do solenóide e apontam ao longo da direção radial.

(e) Não há campo elétrico induzido.

Cada um de dois longos solenoides coaxiais é percorrido por uma corrente elétrica estacionária, de mesma intensidade , porém com sentidos contrários. Ambos os solenoides têm o mesmo comprimento , sendo que o interno possui raio e voltas, ao passo que o externo possui raio e voltas, sendo e .

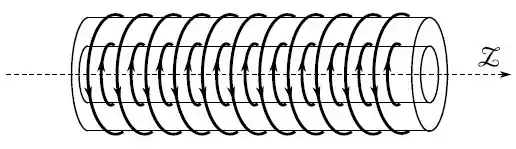
Sendo a distância até o eixo comum dos solenoides, e considerando o campo magnético fora dos dois solenoides igual a , podemos expressar o campo magnético dentro do solenoide interno e entre os dois solenoides , respectivamente, como

; .

; .

; .

; .

; .

Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente estacionária com sentido para fora do plano da página, são colocados um ao lado do outro, formando duas placas finas que se estendem até o infinito, como mostrado na figura abaixo. Cada plano formado possui condutores por unidade de comprimento. Quais são, respectivamente, os módulos dos campos magnéticos produzidos nos pontos , e ?

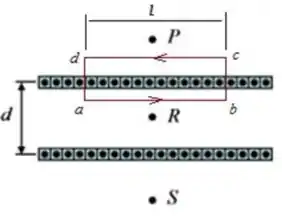
(a), ,

(b), ,

(c), ,

(d), ,

(e), ,

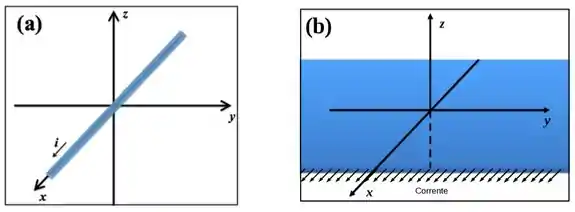
(a) Determine o módulo e descreva as linhas de campo do campo magnético gerado por um fio retilíneo longo conduzindo uma corrente ao longo do eixo (ver figura (a)).

(b) Considere agora uma chapa no plano , que podemos aproximar como infinita, conduzindo uma corrente na direção com densidade uniforme por unidade de largura (ver figura (b)). Utilizando o resultado da letra (a), deduza a direção e o sentido do campo magnético acima e abaixo da placa.

(c) Utilize o resultado do item (b) e a lei de Ampére para calcular o módulo do campo acima e abaixo da placa.

Uma espira circular, com de raio, que conduz uma corrente de , é colocada no centro de um solenóide com de comprimento, de raio e espiras. Determine o valor da corrente no solenóide para que o campo magnético no centro do solenóide seja zero.

1. ;
2. ;
3. ;
4. ;
5. ;

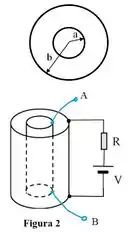
Dois solenoides cilíndricos, de raios e comprimento são colocados um dentro do outro, como mostra a figura ao lado. O solenoide de raio tem espiras por unidade de comprimento e o solenoide de raio possui espiras por unidade de comprimento.

No instante , os terminais do solenoide de raio (o maior) são ligados a uma bateria de . V e um resistor, como mostra a Figura 2.

1. Escreva a expressão para a corrente no solenoide de raio em função do tempo.
2. Escreva a expressão para o fluxo magnético total no solenoide de raio em função do tempo.
3. Escreva a expressão para o módulo da entre os terminais d solenoide de raio , mostrados como e na figura em função do tempo.
4. Suponha que forças externas agindo uniformemente sobre o aro, na direção radial, são responsáveis pelo aumento do raio do aro. Calcule a potência em um certo instante de tempo que as forças externas realizam sobre o aro. Despreze qualquer energia elástica do material que constitui o aro. É possível dizer que ? Justifique sua afirmação.

(Capítulo 29.5 – Exercício 53) Um solenoide longo tem e conduz uma corrente . Um elétron se move no interior do solenoide em uma circunferência de raio perpendicular ao eixo do solenoide. A velocidade do elétron é ( é a velocidade da luz). Determine a corrente no solenoide.

Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.

Determine a auto-indutância por unidade de comprimento do solenóide externo.

Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.

Determine a indutância mútua por unidade de comprimento entre o solenóide externo e o solenóide interno.

Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.

Suponha agora que o solenóide menor seja deslocado perpendicular ao seu eixo por uma distância . Determine a indutância mútua do sistema nessa nova configuração.

Considere um solenóide toroidal de raio médio , com seção transversal de área e voltas de fio enroladas de forma compacta ao longo de seu comprimento.

Suponha que o solenóide é fino, de forma que as dimensões de sua seção transversal sejam pequenas em comparação com . Assim, podemos dizer que o campo magnético é aproximadamente uniforme sobre a seção transversal e coincide com o valor calculado para . Nessas condições, determine a auto-indutância do sistema.

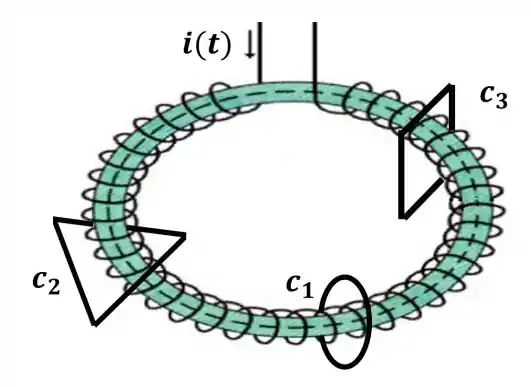
Considere um solenóide toroidal de seção transversal circular de raio . Ele é atravessado por uma corrente de intensidade que varia lentamente com o tempo. Considere também três espiras planas orientadas paralelamente às seções transversais do solenóide: , uma espira circular de raio , , uma espira triangular de lados iguais a e , uma espira quadrada de lado , dispostas no solenóide como mostrado na figura abaixo, envoltas e centralizadas no mesmo. Sejam , e as indutâncias mútuas entre o solenóide e as espiras , e , respectivamente, quando consideradas individualmente. Ordene , e de acordo com os seus módulos.

(I) Calcule o módulo do campo magnético produzido por um solenóide muito longo com espiras por unidade de comprimento, percorrido por uma corrente . Despreze efeitos de borda.

(II) Dois solenóides muito longos, coaxiais, cujos eixos coincidem com o eixo , transportam, cada um, uma corrente porém com sentidos opostos, como mostra a figura. O solenóide de raio tem espiras por unidade de comprimento e o de raio tem espiras por unidade de comprimento. Despreze efeitos de borda.

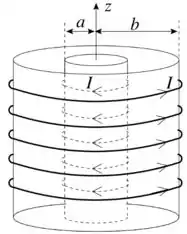
(a) Determine o vetor para .

(b) Determine o vetor para .

(c) Determine o vetor para .

A figura abaixo mostra uma bobina toroidal com espiras bem compactadas. Uma corrente percorre o enrolamento desta bobina.

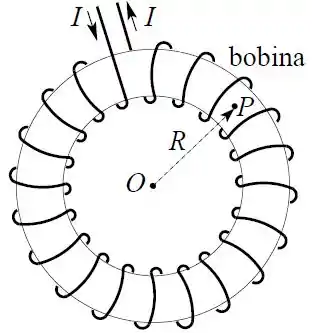
Calcule o módulo do campo magnético em um ponto no interior da bobina, a uma distância do seu eixo, quando a bobina é constituída só pelo enrolamento (núcleo de ar). Lembre que para o magnetismo o ar é praticamente indistinguível do vácuo.

Calcule a relação entre as correntes e na bobina com núcleo de ar e com núcleo de ferro , respectivamente que produzem o mesmo campo magnético no ponto .

Calcule a suscetibilidade do alumínio se com o núcleo de alumínio e mesma corrente o campo magnético no ponto passa a ser do valor no ar. Como se designa esse elemento segundo sua propriedade magnética?

A porção superior da figura abaixo mostra parte de um toróide de seção retangular, de raio interno , raio externo e espessura . Tal toróide contém espiras conectadas, percorridas por uma corrente elétrica . Uma ilustração representativa da configuração geométrica de todo o toróide é dada na porção inferior da figura. Considere que a permeabilidade magnética do vácuo é dada por .

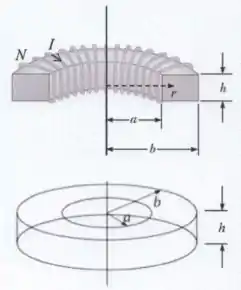
1. Usando a lei de Ampère, calcule o módulo do campo magnético a uma distância do eixo de simetria que passa pelo centro do toróide, onde .
2. Calcule o módulo do fluxo magnético através de uma das espiras retangulares do toróide.
3. Calcule a energia magnética armazenada no interior de todo o toróide.