Oscilações Acopladas
Produzido por Leonardo de BemTeoria
Bom, você já estudou associação entre molas, mas como será que um sistema desses se comporta?
Por exemplo, se o problema te mostrar um sistema assim:
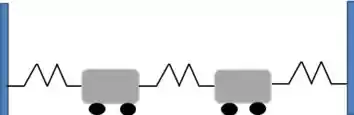
Ou seja, dois carrinhos unidos por três molas. E, a partir dessa configuração malucona, o enunciado te perguntar: “Quais são as frequências de vibração desse sistema?”
É isso que você vai aprender aqui (:
O que são oscilações acopladas?
Bom, o movimento de um carrinho influencia no outro, certo? Porque se um carrinho se mover para frente ou para trás, ele comprime ou distende as molas. Essas molas influenciam no movimento do outro carrinho, não é mesmo?
Dizemos que esse sistema é um sistema de oscilações acopladas. O “Acoplamento” é justamente esse efeito: Os carrinhos não têm movimentos independentes, mas sim dependentes um do outro.
Como resolver esse problema?
Vamos desenvolver uma forma de abordar esse problema em cinco passos:
- Definir o sentido dos deslocamentos e definir as forças do sistema.
- Definir o sistema de EDO’s pela segunda Lei de Newton.
- Usar uma solução padrão e montar a matriz do sistema.
- Calcular o determinante.
- Resolver a equação do segundo grau ou Biquadrada final, obtendo as frequências.

Calma, não é tão complicado assim! Vamos ver cada um desses passos com calma.
Passo 1
Vamos definir o sentido dos deslocamentos no sistema. Pra isso, vamos adotar um sentido positivo para a direita, como sempre fazíamos. A diferença aqui é que vamos considerar dois deslocamentos diferentes:
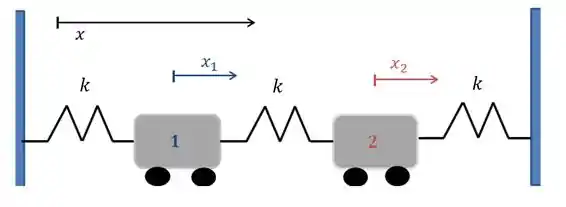
Esses dois deslocamentos são considerados positivos, de início, como você pode ver no sentido deles na figura, ok? Isso facilitará as contas.
Bora analisar primeiro as forças que agem no carrinho
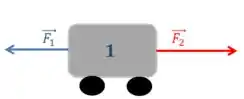
Como estamos considerando deslocamentos positivos, a força 1 vai ser dada pela distensão da mola 1, ou seja:
Certo? Como sempre, a força elástica vai contra o deslocamento. Mas e a força 2? Bom, vamos deixar essa pro final, pois ela depende do outro carrinho.
Agora, pro carrinho 2:
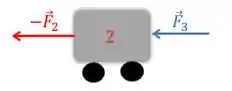
Onde é dada por:
Qual o motivo desse sentido? Bom, novamente, como estamos considerando os deslocamentos positivos, a mola 3 está sendo comprimida. Assim, a força terá o sentido acima, contrário ao sentido positivo do eixo
E agora, a misteriosa força ...
Bom, essa força afeta os dois movimentos, por isso a deixei por último. Vamos fazer mais uma consideração: Que é maior que . Assim, o da mola será dado por:
Ou seja, se os dois carrinhos andarem o mesmo tanto pra direita, por exemplo, a mola entre eles vai continuar na mesma! Essa mola só vai comprimir ou esticar se o deslocamento dos dois carrinhos for diferente.
Agora se houver um deslocamento entre os carrinhos (), então vai ter uma força entre eles, que é essa nossa . Se sobre o nosso carrinho vai ter uma força sobre o nosso carrinho vai ter uma força , ou seja, isso é um par ação-reação.
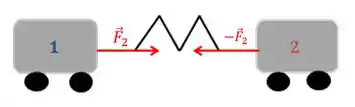
O módulo da força é dado por:
Passo 2
Precisamos agora definir as EDO’s. Vamos começar com o carrinho 1: Olhando os sentidos das forças que nele agem, podemos escrever:
Isolando e
Fazendo a mesma coisa pro carrinho 2:
Assim temos o sistema:
Passo 3
Agora vamos usar uma solução padrão pra manipular nosso sistema. Esse é o nosso pulo do gato.
Como você deve lembrar, a solução de um MHS tem a forma:
Então vamos usar as soluções:
Ambos com a mesma frequência Sim, pois estamos procurando frequências de oscilação comum para todo o sistema. Agora, substituindo essas equações no sistema de EDO’s e lembrando que:
Pô, mas esse é , né? Então a gente pode rescrever
Vamos chegar ao resultado abaixo:
Beleza? Agora vamos escrever isso na forma matricial (dá um pulinho lá em álgebra linear, caso não lembre 😉):
Passo 4
Pela equação matricial dali de cima, podemos ver que existe a solução:
Porém, não a queremos, não é mesmo? Porque isso geraria:
Pra que isso não aconteça, o determinante da matriz maior precisa ser nulo. Assim:
O que nos leva à equação:
A equação acima é chamada de equação de frequência ou equação característica do sistema.
Passo 5
Precisamos resolver a equação biquadrada. Como faz isso mesmo? É assim:
Na equação acima, você chama:
E assim ela se transforma em:
Dai você resolve essa equação do segundo grau e, com os valores de , você acha
Vamos fazer isso na nossa equação de frequência (só que aqui vamos usar as variáveis
Onde:
Assim:
Com os valores de , você calcula as frequências:
Preste atenção nessa última equação: só tomaremos os valores positivos de . Devemos fazer isso porque as frequências são, por definição, positivas!
Ufa! Terminamos. Você só deve prestar atenção em duas coisas:
- Os valores de precisam ser positivos (afinal de contas, depois você vai tirar a raiz deles depois)
- Os valores de também precisam ser positivos.
Nesse nosso exemplo fizemos com que as massas fossem diferentes e constantes de molas fossem iguais, mas o seu professor pode inventar um montão de coisas!!! :o
Vamos ver como seria o caso com constantes de mola diferentes:
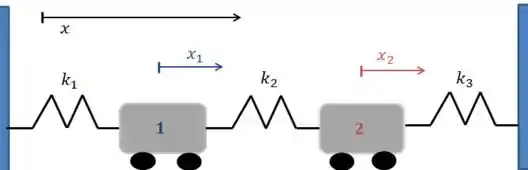
O nosso sistema de EDO’s ficaria assim
Já que sobre o bloco vão atuar as molas de constantes elásticas e e sobre o bloco vão atuar as molas de constantes elásticas e !
Uma vez montado esse sistema é só seguir o passo-a-passo e correr pro abraço! \o/
E é isso, bora fazer uns exercícios pra fixar isso bem (:
Passo 2
Passo 3
Passo 4
Passo 5
Exercícios Resolvidos
Exercício Resolvido #1
USP-P1-2014-Q5
Considere um sistema formado por duas partículas idênticas de massa ligadas por uma mola de massa desprezível e constante elástica . Supondo que as partículas se movem em apenas uma direção e a única força atuante no sistema advém da mola, assinale a alternativa correta para a frequência angular de oscilação.
Passo 1
Bom, nessa questão temos um caso de uma oscilação acoplada usando apenas uma mola. Além disso, nas extremidades da mola temos massas iguais.
Qual a primeira conclusão que podemos tirar disso? Simetria! Já que temos uma mola e duas massas iguais, podemos esperar que o que gera o movimento de uma massa gera o da outra.
Assim, podemos esperar deslocamentos iguais das massas:
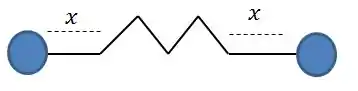
Passo 2
Além disso, quais deverão ser os sentidos dos deslocamentos? Os deslocamentos não podem ter o mesmo sentido.
Qual o motivo disso? Porque o centro de massa precisa ter aceleração nula, logo, o somatório de forças agindo nele deve ser nulo. Isso ocorre porque não temos nenhuma força externa atuando no sistema. Assim, devemos esperar o seguinte sistema de forças:
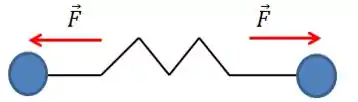
Ou:
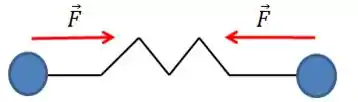
Pra que isso ocorra, quando uma massinha andar a outra deve andar , no sentido contrário. Os deslocamentos são os mesmos em módulo para que as forças sejam iguais. Temos um caso simétrico.
Passo 3
Mas pera ai, se uma massinha anda pra um lado e pro outro, qual a distorção total da mola?
Bom, vai ser a soma dos módulos desses deslocamentos, ou:
Assim, podemos dizer que a força elástica que age em cada massinha é do tipo:
Passo 4
Beleza, então podemos dizer que, pra cada massinha:
Como as duas equações são iguais, não precisamos montar um sistema de EDO’s, calcular determinante, resolver a equação biquadrada, etc. Basta que a gente resolva uma delas, pois vai valer para as duas massas:
Lembrando da definição de frequência:
Pronto!
Resposta
d)
Exercício Resolvido #2
Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Considere dois osciladores harmônicos idênticos com constantes de mola e acoplados por uma mola muito fraca com constante . A variação na frequência de vibração do modo antissimétrico com relação ao modo simétrico vale aproximadamente?
Dica: Usar a aproximação: , quando .
Passo 1
O sistema pode ser representado pela figura abaixo:
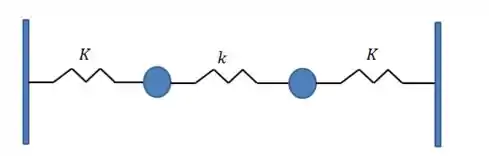
Passo 2
Bom, o enunciado cita dois modos de vibração: o simétrico e o antissimétrico. Vamos seguir o passo a passo para achar as frequências dos modos de vibração.
Primeiro, vamos adotar deslocamentos positivos e para as massas:
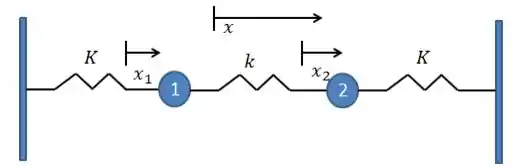
Considerando que , a mola central estará sendo esticada e o módulo da força elástica que a mesma gerará nas massas será:
O sentido das forças em cada massa será:
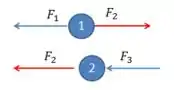
Passo 3
Bora escrever as EDO’s agora, usando o sentido adotado para cada força:
Para a massa 1:
Para a massa 2:
Reescrevendo e isolando
Passo 4
Usando as soluções padrões:
Substituindo e lembrando que:
Assim:
Cortando todos os cossenos:
Passo 5
Escrevendo o sistema na forma matricial:
Como não queremos a solução trivial, o determinante da matriz acima tem que ser nulo:
Assim:
E:
A frequência do modo simétrico será a menor e a frequência do modo assimétrico é a maior:
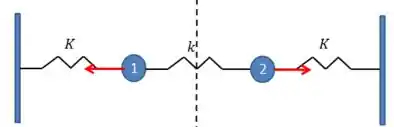
O modo assimétrico é aquele em que os corpos apresentam deslocamentos diferentes(como no caso abaixo, em que os deslocamentos têm sentidos diferentes):
E o simétrico, deslocamentos iguais:
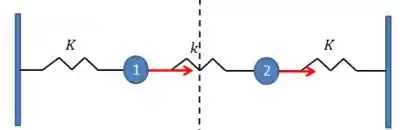
Passo 6
Queremos saber a variação do modo antissimétrico em relação ao modo simétrico. Quer dizer que queremos calcular:
Assim:
Beleza? Como , , assim, podemos usar a aproximação:
Usando:
Vamos ter:
Substituindo em
Resposta
Exercício Resolvido #3
USP-P2-2014-Q1
Dois pêndulos, cada um composto por um fio de comprimento prendendo uma partícula de massa , realizam um movimento harmônico simples (pequenas amplitudes) com uma mola de constante elástica e massa desprezível unindo as massas no plano de oscilação. Quais o modos normais de oscilação?
- e
- e
- e
- e
- e
Passo 1
Bom , o sistema com que estamos lidando pode ser representado pela figura abaixo:
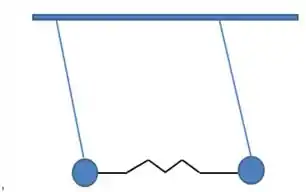
Podemos chamar de o deslocamento horizontal que a primeira massinha sofre, e de o ângulo que o pêndulo faz com a vertical. Da mesma forma, podemos chamar de e o deslocamento e o ângulo da massinha 2.Assim:
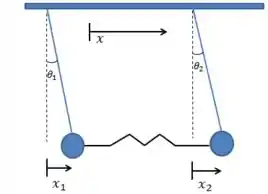
Estamos considerando ambos os deslocamentos positivos, como costumamos fazer.
Passo 2
Agora precisamos descobrir as forças que agem em cada bolinha. Vamos primeiro analisar as forças devido aos pêndulos.
Lembra como chegar na força que age num pêndulo simples? Nós costumamos decompor o peso na direção , o que gera:
Se não lembra bem, dá um pulinho lá no tipo de pêndulos simples.
Então as forças devido ao pêndulo simples serão do tipo escrito acima. Porém, temos também a força que a mola exerce em cada massa.
Vamos considerar que , com isso a mola estará sendo esticada, e a força que a mola exerce em cada massa terá o sentido abaixo:
O módulo da força será dado por:
Passo 3
Seguindo o sentido que cada força tem, podemos escrever:
Para a massa 1:
Para a massa 2:
Bora usar agora a velha e boa aproximação para pequenos ângulos:
Assim:
Reorganizando as equações:
E temos o nosso sistema de EDO’s.
Passo 4
Agora vamos supor que as soluções são do tipo:
Substituindo nas equações e lembrando que:
Teremos:
Cortando todos os cossenos:
Isolando e
Passo 5
Agora vamos escrever o sistema na forma matricial:
Como não queremos a solução trivial ( o determinante da matriz acima tem que ser nulo. Assim:
Assim:
Então:
E:
Então a resposta é:
e)
Resposta
e)
Exercício Resolvido #4
USP-P2-2014-Q6
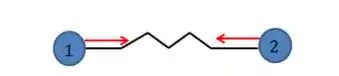
Dado um sistema de duas partículas de massa ligados por três molas de constante elástica e massa desprezível, como ilustrado abaixo:
O sistema possui dois modos normais de vibração, e , onde . Quando o sistema oscila com frequência ou , a frequência de oscilação do centro de massa é respectivamente
- e
- e
- e
- e
- e
Passo 1
Nessa questão, as frequências dos modos de vibração já foram dadas. Assim, você não precisa seguir todos aqueles passos pra encontra-las. Porém, o que o enunciado te pede é a frequência de vibração do centro de massa em cada caso.
Bom, pelo arranjo das massas, não podemos esperar muitas formas de movimentação delas.
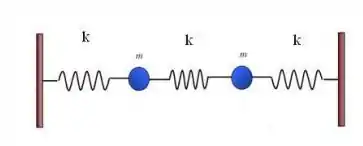
No primeiro caso, em que o sistema vibra no primeiro harmônico, temos a seguinte configuração:
Isso para . Nesse caso, quando uma mola for comprimida por metros, a outra vai ser distendida por metros.
Porém, como o módulo de é o mesmo, já que as massas são as mesmas, a mola central não sofrerá nenhuma alteração:
Ou seja, enquanto uma mola é comprimida metros da esquerda para a direita, a outra é estendida em metros da esquerda para a direita. Isso não gera folgas e, portanto, a mola central não tem seu comprimento alterado.
Então ela se comportar como se fosse uma massa qualquer e vai oscilar com a mesma frequência que as molas: .:
Passo 2
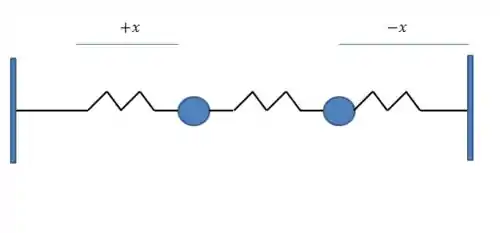
No segundo caso, o esquema fica assim:
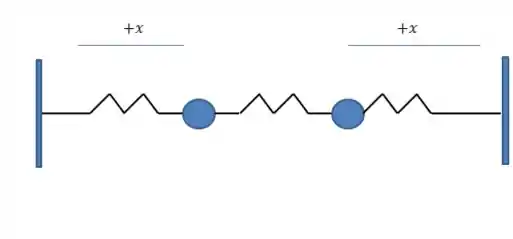
Nesse caso, enquanto uma mola for comprimida, a outra também será comprimida. Enquanto uma for esticada, a outra também será esticada. Isso fará com que a mola do centro sofra alterações no seu comprimento.
Só que tem uma coisa: Estamos analisando o centro de massa, certo?
Pense então: Como as molas são iguais, o que uma sofrer de compressão a outra também sofrerá. Como as forças geradas serão iguais, o centro de massa da mola central não mudará de posição.
Isso pode ser visto calculando-se a somatória das forças sobre o centro de massa:
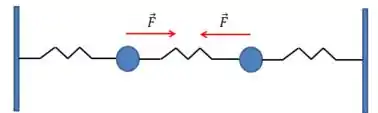
Por que as forças têm sentidos contrários. Assim, como o centro de massa não sofre nenhuma força resultante, a sua posição não muda e não oscila:
Resposta
e)
Exercício Resolvido #5
USP-P2-2014-Q4
Uma cadeia linear de partículas de massa , ligadas com molas de constante elástica e massa desprezível, precisa de quantas condições iniciais para a completa descrição do sistema? Considere apenas deslocamentos longitudinais.
Passo 1
Bom galera, pra resolver a equação de um MHS do tipo:
Nós precisamos geralmente de duas condições:
Uma velocidade inicial e um espaço inicial, certo?
Assim a gente consegue descrever completamente o sistema.
Agora, um sistema composto por molas, é um sistema complexo formado por MHS, ou seja, quantas condições vamos precisar ter pra descrever todo o sistema?
A resposta é . Duas condições para cada MHS. (:
Resposta
e)