Exercícios de Método dos Fasores - Lista de Exercícios Resolvida

Duas fontes emitem campos elétricos na mesma direção e de mesma frequência com amplitudes iguais a .

Os campos interferem num ponto em que a diferença de fase entre eles é de .

A amplitude resultante será (dica: use fasor):

Obtenha o campo elétrico resultante da soma vetorial dos seguintes campos elétricos em uma interferência produzida por um dispositivo com três fendas:

Cinco ondas eletromagnéticas senoidais de mesma amplitude incidem num detector, cujos campos elétricos, neste ponto, são dados por:

A amplitude do campo elétrico resultante no detector é dada por:

6. Nenhuma das anteriores

Obtenha o campo elétrico resultante da soma vetorial dos seguintes campos elétricos em uma interferência produzida por um dispositivo com três fendas:

Num arranjo experimental os pontos e funcionam como fontes de luz idênticas emitindo em fase com comprimentos de onda .

A distância entre e pode ser variada, e encontra-se a uma distância do anteparo.

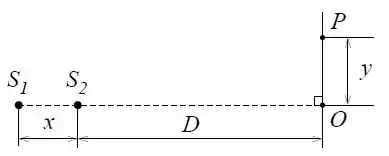
1. Obtenha a expressão para a diferença de fase entre as ondas no ponto . (obs: NÃO faça nenhuma aproximação).
2. Para que valores de obtém-se interferência destrutiva para (ponto )?
3. Se apenas um dos ou estiver presente a intensidade observada no ponto do anteparo é aproximadamente constante e igual a para e pequenos (as amplitudes dos campos elétricos devidos às fontes em são aproximadamente iguais: ).

Deduza a expressão da intensidade resultante observada no ponto como função apenas de e .

Seja um sistema de fenda dupla tal que a distância entre as fendas é e a distância até um anteparo é , como mostrado na figura. A partir da esquerda e direção perpendicular à fenda, incide uma onda luminosa de comprimento de onda . Para ângulos não muito grandes, seja a intensidade da luz no anteparo quando apenas uma fenda está aberta.

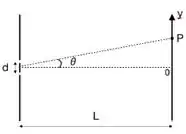
a) Obtenha, pelo método que escolher, a intensidade da luz no anteparo quando as fendas estão abertas, em função do ângulo e em função de .

b) Faça um esboço, em função de , da intensidade da luz no anteparo. Admita que vale a aproximação de pequenos ângulos.

c) Seja , e . Encontre quais são as posições em , entre os máximos de ordem e , para os quais a intensidade é metade da intensidade máxima.

d) Inserindo uma lâmina de vidro com índice de refração e espessura em uma das fendas, de quanto se desloca a posição do máximo central no anteparo?

– Obtenha o campo elétrico resultante da soma vetorial dos seguintes campos elétricos em uma interferência produzida por um dispositivo com três fendas:

Em determinado ponto no espaço observa-se que a superposição de ondas planas eletromagnéticas monocromáticas produz um campo elétrico cuja amplitude é:

Afirmamos então que pode ser escrito de maneira mais compacta como , onde , e é igual a:

Considere quatro ondas eletromagnéticas planas, monocromáticas e linearmente polarizadas propagando-se no vácuo cujos campos elétricos em um ponto sejam dados pelas seguintes expressões:

Que condições devem ser satisfeitas para que o campo elétrico resultante neste ponto seja nulo?

O campo elétrico nesse ponto não pode ser nulo sob quaisquer condições.

O campo elétrico nesse ponto é sempre nulo.

Nenhuma das alternativas anteriores está correta.

Em um experimento de Young, observa-se a intensidade da luz em um anteparo a da fenda dupla. O feixe incidente tem comprimento de onda . Observa-se que, a partir do eixo central, a terceira mancha escura está a uma distância de do centro da figura de interferência.

a) Qual a diferença de caminho ótico entre os raios que chegam no ponto médio dessa terceira mancha escura?

b) Qual é a distância entre as fendas?

Suponha que agora há três fendas, equidistantes de . Faça as questões a seguir literalmente, tomando como conhecido .

c) Escreve a expressão para o campo elétrico total em um ponto na tela, com abertura angular em relação ao eixo central, escrevendo o campo elétrico da primeira fenda (a mais superior) da forma e considerando a diferença de fase pelas fendas subsequentes.

d) Mostre, via método de soma de fasores, que a intensidade da luz em um ponto da tela de observação é dada por , onde .

Cinco ondas eletromagnéticas senoidais de mesma amplitude incidem num detector, cujos campos elétricos, neste ponto, são dados por:

A amplitude do campo elétrico resultante no detector é dada por:

Nenhuma das anteriores

Considere as afirmações a seguir sobre o experimento de Young, para o qual as larguras das fendas são desprezíveis, e marque a alternativa CORRETA.

I) O padrão de intensidade observado no plano distante das fendas é explicado através da diferença de caminho óptico percorrido por cada um dos dois feixes de luz.

II) O padrão de intensidade observado se mantém inalterado, tanto em magnitude quanto nas posições das franjas, mesmo quando se adiciona uma fase relativa entre os feixes que saem de cada fenda.

III) A intensidade da onda em um ponto qualquer no plano de observação é igual à soma das intensidades dos feixes que saem das fendas, na posição considerada.

(a) Apenas I está correta.

(b) Apenas II está correta.

(c) Apenas III está correta.

(d) Apenas I e II estão corretas.

(e) Apenas I e III estão corretas.

(f) Apenas II e III estão corretas.

(g) Nenhuma está correta.

Duas fontes emitem campos elétricos na mesma direção e de mesma frequência com amplitudes iguais a .

Os campos interferem num ponto em que a diferença de fase entre eles é de .

A amplitude resultante será (dica: use fasor):