Redes de Difração
Produzido por Bruno SoaresTeoria
O que faz os CDs funcionarem?
Vamos voltar a falar de CDs.

Um CD tem, na parte de baixo, vários sulcos. Eles são compostos pelo que chamamos de “ilhas” e “poços”, que são elevações e vales nos CDs ao longo de uma trilha em espiral que o seu computador vai lendo.
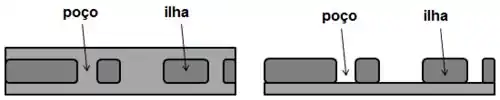
Os poços funcionam como as fendas da interferência e difração de fendas!
Assim, o CD é na verdade um conjunto com um número enorme de fendas paralelas, que podemos dizer que têm aproximadamente a mesma largura e a mesma distância entre os centros de duas fendas consecutivas.
Um conjunto com uma quantidade enorme de fendas paralelas é chamado de rede de difração. Essa rede é na verdade um experimento de difração por fendas, onde é ENORME. ( fendas é pequeno para o que chamamos de ENORME).
Às vezes, essas fendas também são chamadas de linhas, por serem muito pequenas, quase pontuais.
Quando isso acontece, as nossas franjas de interferências vão ficando menos largas, virando linhas.
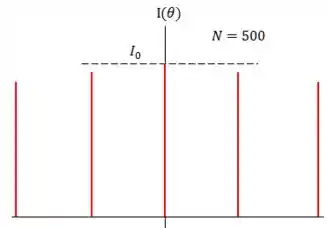
Nesse arranjo, novamente, os máximos são calculados pela relação
Essa fórmula é na verdade um agente duplo:
- Quando iluminamos a rede com uma luz monocromática, a figura obtida é constituída por uma série de linhas em ângulos determinados por ela.
- Quando iluminamos a rede de difração com luz branca (que possui vários comprimentos de onda), podemos determinar o ângulo para cada cor através da equação acima.
As linhas são chamadas de linhas de primeira ordem, as linhas são chamadas de linhas de segunda ordem, e assim por diante.
É isso que acontece quando olhamos um CD.

Como cada cor tem um comprimento de onda, os ângulos das linhas mudam para cada uma delas, e aí o CD decompõe a luz branca em todas as suas cores.
Como agora temos uma quantidade absurdamente grande de fendas, vamos parar de falar por exemplo que eu tenho fendas e falar que eu tenho em uma rede que tem de comprimento.
Qual a distância entre duas fendas consecutivas?
Sabemos que essa distância é sempre igual a . Se eu tenho fendas, a distância total entre elas é . Essa distância total é o comprimento da rede! A distância entre duas fendas vai ser que dá .
Agora façamos isso de uma forma mais geral.
Vamos chamar o número de fendas por unidade de comprimento de .
Assim, se tivermos fendas em uma rede com comprimento :
Como o comprimento da rede é a distância total entre as fendas, .
E o nosso agente duplo muda de forma! Ele está evoluindo!
Sua equação evoluiu para:
Observação:
Como em geral é um valor grande, quando trabalharmos com redes de difração, os ângulos serão grandes. Isso significa que não podemos mais usar nossa aproximação de pequenos ângulos. Ou seja
Redes de Difração com Luz Incidente Inclinada
Quando a luz incide numa rede de difração, seus raios podem vir de qualquer direção, fazendo diferentes ângulos com a rede.
Quando isso acontece, as condições para interferência construtiva (as posições das franjas brilhantes) são diferentes de quando a luz incide perpendicularmente à rede e ficam:
Onde é o ângulo de incidência da luz e é o ângulo de saída da luz.
Qual a diferença de ir de 2 para milhares de fendas?
Quando o número de fendas aumenta muito, os máximos principais da figura de interferência vão se estreitando, até se tornarem linhas.
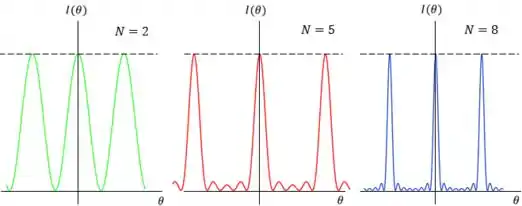
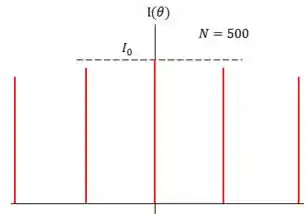
Mas o quanto essas linhas são realmente “linhas”, e não franjas largas?
Na verdade, a largura de metade da franja é dada por:
Onde é o número de fendas, é a distância entre duas fendas consecutivas e é o ângulo que corresponde a nossa linha.
Vamos ver na nossa rede com que distam das consecutivas, uma luz com um comprimento de onda de para a linha de ordem 1
Para esta linha, temos:
Assim, a meia largura é dada por:
Mas
Ou seja, é praticamente uma linha mesmo.
Para a linha central (linha de ordem 0), o ângulo é , e logo a meia largura vai ser:
Intensidade das Franjas
A rede de difração, embora tenha um número absurdamente grande de fendas, continua sendo um caso de difração por um número de fendas.
Logo, embora sua figura de interferência seja composta por várias linhas:
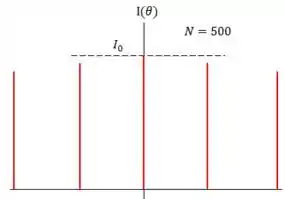
A altura dessas linhas é dada pela mesma fórmula da intensidade de difração por fendas.
Onde é a largura de cada fenda, é a distância entre duas fendas consecutivas, é o desvio angular do ponto e é o comprimento de onda da luz incidente.
Além disso, a intensidade máxima da figura é dada por:
E isso acontece na franja central.
Também temos que:
- Existem máximos secundários entre cada par de máximos principais.
- Existem mínimos entre cada par de máximos principais, esses pontos são encontrados quando , .
Porém, nesse caso, esses máximos secundários vão ser muito pequenos em comparação com as linhas de interferência.
Rede de Difração com Vários Comprimentos de Onda
Na rede de difração, a posição das linhas é dada por:
Ou
Essas posições dependem diretamente do comprimento de onda da luz utilizada. Mas e se a luz for branca, que possui vários comprimentos de onda?
A posição das linhas de cada cor vai ser dada pela equação acima para cada comprimento de onda! Assim, você vai ver a luz branca virar linhas coloridas. Uma forma de ver isso é apontar uma lanterna de LED branca para certos tipos de TV.

Simbora pros exercícios?
Redes de Difração com Luz Incidente Inclinada
Qual a diferença de ir de 2 para milhares de fendas?
Intensidade das Franjas
Rede de Difração com Vários Comprimentos de Onda
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-46
Talvez para confundir os predadores, alguns besouros girinídeos tropicais são coloridos por interferência ótica produzida por escamas cujo alinhamento forma uma rede de difração (que espalha a luz em vez de transmiti-la).
Quando os raios luminosos incidentes são perpendiculares à rede de difração o ângulo entre os máximos de primeira ordem (localizados dos dois lados do máximo de ordem zero) é aproximadamente para uma luz com um comprimento de onda de .
Qual é a distância efetiva entre as ranhuras da rede de difração?
Passo 1
Para redes de difração, os máximos continuam sendo dados por:
Onde é a distância entre duas ranhuras da rede.
A distância entre os dois máximos de primeira ordem é dada por . Mas como podemos ver na fórmula, já que , teremos que, em módulo, os ângulos entre os máximos e o centro da figura serão iguais.
Logo, para o máximo com , seu ângulo é:
Passo 2
Rearranjando a condição de máximo de interferência:
Avaliando o máximo de primeiro ordem (), que tem ângulo para uma luz com comprimento de onda :
Resposta
A distância efetiva entre as ranhuras da rede de difração é .
Exercício Resolvido #2
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-87
Uma rede de difração com de largura produz um máximo de segunda ordem a quando o comprimento de onda da luz é .
Qual é o número de fendas da rede?
Passo 1
O ângulo do máximo de segunda ordem da rede de difração é dado por:
O enunciado nos diz que:
Rearranjando e substituindo:
Passo 2
Como temos , o número de fendas da nossa rede, que tem de largura, é:
Resposta
Exercício Resolvido #3
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-97
Uma rede de difração tem fendas em . Se uma luz com um comprimento de onda de incide na rede, quantas ordens (máximos) existem de cada lado do máximo central?
Passo 1
Os máximos da rede são dados por:
Temos o número de linhas por centímetro da nossa rede, que é:
E o comprimento de onda da luz incidente
Passo 2
O maior máximo que ainda vai existir na nossa figura tem que ter um ângulo menor que .
No caso de , a ordem seria:
O último máximo que aparece é o máximo de ordem . Aparecem então máximos de cada lado do máximo central, mais o máximo central, somando máximos.
Resposta
Existem dois máximos de cada lado do máximo central.
Exercício Resolvido #4
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-47
Uma rede de difração com de largura possui ranhuras. Uma luz com um comprimento de onda de incide perpendicularmente na rede. Determine:
- O maior valor de para o qual são observados máximos em uma tela distante.
- O segundo maior valor de para o qual são observados máximos em uma tela distante.
- O terceiro maior valor de para o qual são observados máximos em uma tela distante.
Passo 1
Primeiro, vamos calcular o número de ranhuras por milímetro dessa rede.
E lembrando que o comprimento de onda da luz incidente é
Passo 2
Letra a)
Precisamos encontrar a ordem do último máximo a aparecer na tela, aquele cujo ângulo é o maior possível que ainda seja menor que .
Para acharmos isso:
Ou seja, o último máximo é o de ordem .
Seu ângulo será dado por:
Passo 3
Letra b)
O segundo maior valor de vai ser o do máximo de segunda maior ordem, .
Passo 4
Letra c)
O terceiro maior valor de vai ser o do máximo de terceira maior ordem, .
Resposta
Letra a)
Letra b)
Letra c)
Exercício Resolvido #5
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-91, modificado
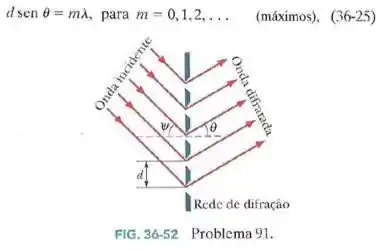
Uma luz incide em uma rede de difração fazendo um ângulo com o plano da rede, como mostra a Fig.36-52. Mostre que franjas claras ocorrem em ângulos que satisfazem a equação
, para
(Compare essa equação com a Eq.36-25). Apenas o caso especial foi tratado.
Passo 1
Precisamos apenas verificar a diferença de fase entre duas fendas, pois todas as fendas têm mesma distância até sua vizinha.
Quando a luz chega inclinada à rede de difração, os raios têm uma diferença de fase causada pela diferença de percurso.
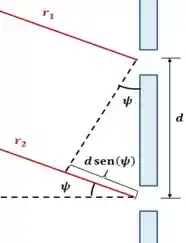
Pela imagem, vemos que a diferença de percurso é de .
A diferença de fase em múltiplos do comprimento de onda é:
Passo 2
A luz sai da rede de difração com um ângulo para atingir um ponto qualquer num anteparo longe. Para podermos visualizar a diferença de fase:
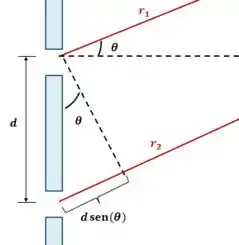
A diferença de percurso na saída vai ser:
Passo 3
A diferença de fase total vai ser a soma das duas:
Quando a diferença for um múltiplo inteiro do comprimento de onda, teremos um máximo de interferência. Ou seja:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-92, modificado
Uma rede de difração com é iluminada por uma luz com um comprimento de onda de para vários ângulos de incidência.
Faça um gráfico (para o intervalo de a ) do ângulo entre a direção do máximo de primeira ordem e a direção de incidência em função do ângulo de incidência.
Passo 1
O ângulo entre a direção do máximo e a direção de incidência é .
Como estamos no primeiro máximo, temos:
Onde usamos .
O ângulo vai ser:
Passo 2
O ângulo buscado em função do ângulo de incidência vai ser:
Passo 3
Fazendo o gráfico do resultado:
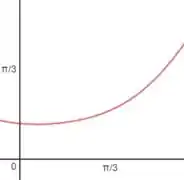
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-50
Uma rede de difração é feita de fendas com de largura, separadas por uma distância de . A rede é iluminada com luz monocromática de comprimento de onda e a incidência é normal.
- Quantos máximos são observados na figura de difração?
- Qual é a largura da linha observada na primeira ordem se a rede possui fendas?
Passo 1
Letra a)
Para achar o maior máximo observado:
Logo, o maior máximo corresponde a . Isso significa que teremos 3 máximos observado:
O máximo central e um de cada lado dele.
Passo 2
Letra b)
A largura das linhas observadas na figura de difração é:
Inicialmente, vamos achar o ângulo da linha. Na primeira ordem, o ângulo é dado por:
Passo 3
Como temos fendas, a meia largura será dada por:
Resposta
A linha terá uma semi-largura de e uma largura de .
Exercício Resolvido #8
UFRJ, Física 4, Prova 1, 2009.1
Considere uma rede de difração com ranhuras por milímetro. A rede é iluminada com um feixe estreito de luz verde , que incide perpendicularmente sobre a mesma.
Os feixes têm intensidade e diâmetro igual a . O padrão de interferência é formado sobre um anteparo paralelo à rede de difração situado a de distância.
- Calcule o número de ranhuras que atuarão efetivamente como fontes secundárias (ou fontes de Huygens) nesta experiência.
- Calcule o valor máximo da razão .
- Calcule a diferença angular entre os dois mínimos adjacentes ao máximo central.
- Quantos zeros há entre o máximo central e um máximo de primeira ordem?
- Escolha uma escala apropriada e faça um esboço do gráfico da razão em função de representando o máximo central e a disposição do primeiro zero.
Passo 1
Letra (a): Calcule o número de ranhuras que atuarão efetivamente como fontes secundárias (ou fontes de Huygens) nesta experiência.
Como a rede de difração possui 400 ranhuras por milímetro e é iluminada por um feixe de diâmetro igual a , somente as ranhuras iluminadas atuarão como fontes secundárias, logo.
Passo 2
Letra (b): Calcule o valor máximo da razão .
O maior valor da razão se dará no maior valor possível de , isso acontece justamente no máximo central.
Quando falamos de intensidade, vimos que o valor dos máximos principais são proporcionais a , assim, no máximo central:
Logo:
Passo 3
Letra (c): Calcule a diferença angular entre os dois mínimos adjacentes ao máximo central.
Os ângulos em que encontramos mínimos de interferência são dados por:
Assim, a diferença angular entre os dois mínimos adjacentes ao máximo central será:
Onde , logo:
Passo 4
Letra (d): Quantos zeros há entre o máximo central e um máximo de primeira ordem?
Conforme vimos em Interferência e em Difração para fendas, entre cada dois máximos principais existem zeros.
Logo:
Passo 5
Letra (e): Escolha uma escala apropriada e faça um esboço do gráfico da razão em função de representando o máximo central e a disposição do primeiro zero.
Algumas informações que já temos de antemão é que, para fendas, a altura do máximo central é proporcional a , e que a largura do máximo central é proporcional a .
Assim, um gráfico apropriado de é algo do tipo:
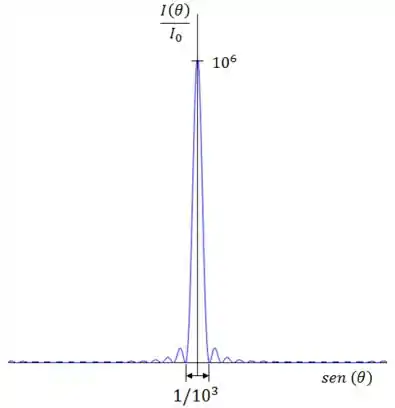
Lembrando que, nesse tipo de questão, não é necessário que você faça algo exatamente igual, mas é importante colocar algumas informações que você já possui. ;)
Resposta
Letra (a):
Letra (b):
Letra (c):
Letra (d):
Letra (e):
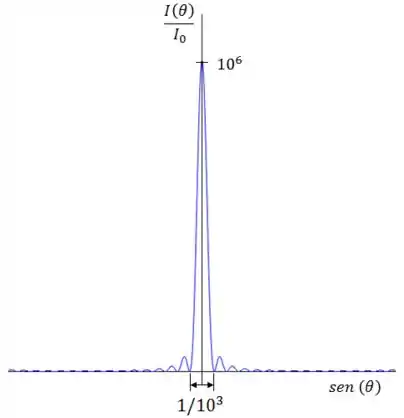
Exercício Resolvido #9
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-98
Uma rede de difração com de largura possui fendas paralelas. Uma luz monocromática que incide perpendicularmente na rede sofre uma difração de em primeira ordem.
Qual é o comprimento de onda da luz?
Passo 1
Para a rede de difração, os máximos ficam nos ângulos dados por:
Rearrumando, podemos encontrar o comprimento de onda da luz:
Passo 2
A rede tem fendas em , logo:
Além disso, o máximo de primeira ordem () está a um ângulo de . Substituindo:
Resposta
Exercício Resolvido #10
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 145-112
Quantas ordens do espectro visível ( a ) podem ser produzidas por uma rede de difração de ?
Passo 1
Os máximos de uma rede de difração são dados por:
Para encontrar o máximo de maior ordem de um dado comprimento de onda, nós substituímos o ângulo por , obtendo um limite superior.
Passo 2
Pelo enunciado:
E como vemos, quanto maior o comprimento de onda, menos ordens de máximo irão aparecer na figura. Então, vejamos o limite para o maior comprimento possível da nossa faixa,
Substituindo:
A maior ordem que aparece para o nosso comprimento de onda é . Isso significa que para todo o espectro visível aparecem no máximo 2 ordens de máximo.
(Para outros comprimentos de onda do espectro visível podem aparecer máximos com ordem maior que , porém ao falarmos de todos os comprimentos de onda, só podemos garantir o surgimento de máximos de ordem até ).
Resposta
Apenas ordens do espectro visível podem ser produzidas.
Exercício Resolvido #11
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 142-55
Uma rede de difração tem ranhuras por milímetro e é iluminada por luz branca com incidência normal. Uma figura de difração é observada em uma tela, a da rede.
Se um furo quadrado com de lado é aberto na tela com o lado interno a do máximo central e paralelo a esse máximo, determine:
- O menor comprimento de onda da luz que passa pelo furo.
- O maior comprimento de onda da luz que passa pelo furo.
Passo 1
Letra a)
Para redes de difração, as franjas brilhantes são dadas por:
Assim, a ordem do máximo que apareceria no buraco para um dado comprimento de onda é:
Digamos que apenas o máximo de uma dada ordem aparecesse. Nesse caso, quanto mais longe do centro da figura a luz batesse, maior precisaria ser o comprimento de onda para produzir uma franja no lugar.
Assim, o menor comprimento de onda que passa pelo furo vai passar pelo lado interno do furo.
Passo 2
Como o lado interno do furo está a uma distância de do centro da tela, que está a da rede de difração, o ângulo dele será:
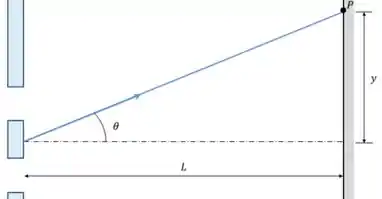
Lembrando que o enunciado nos diz que:
Substituindo:
Para a luz branca (espectro visível), considera-se em geral os comprimentos de onda de a e, nessa faixa, o único valor que nos dá um valor inteiro nessa divisão é
Passo 3
Letra b)
Iremos repetir o que fizemos para a letra a, mas dessa vez com a borda superior do furo ( quanto mais longe do máximo central, maior o comprimento de onda).
Neste caso, a altura é
E o valor máximo de comprimento de onda que passa pelo furo é .
Resposta
Letra a)
Letra b)
Exercício Resolvido #12
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 142-51
Uma luz de comprimento de onda incide normalmente em uma rede de difração. Dois máximos de difração vizinhos são observados em ângulos dados por e .
Os máximos de quarta ordem estão ausentes.
- Qual é a distância entre fendas vizinhas?
- Qual é a menor largura possível das fendas?
- O maior valor do número de ordem dos máximos produzidos pela rede.
- O segundo maior valor do número de ordem dos máximos produzidos pela rede.
- O terceiro maior valor do número de ordem dos máximos produzidos pela rede.
Para a largura da letra (b), determine:
Passo 1
Letra a)
O enunciado nos diz que temos máximos vizinhos com ângulos dados por e .
A condição de máximos para a rede de difração é:
Substituindo o comprimento de onda , temos para o primeiro:
Como o segundo é consecutivo, .
Passo 2
Letra b)
Para os máximos de quarta ordem estarem ausentes, eles precisam ser coincidentes com um mínimo de difração. Os mínimos de difração são dados por:
Igualando com a condição para o máximo de quarta ordem.
Rearranjando, a largura das fendas será:
Para que seja o menor possível, tem que ser o menor possível. Por isso .
Passo 3
Letra c)
Para achar a maior ordem na figura de difração, temos que ver qual seria a ordem de um hipotético máximo em , e usar a maior ordem menor que essa.
Logo, a maior ordem que aparece é .
Passo 4
Letra d)
A segunda maior ordem seria . Contudo, o enunciado nos diz que a quarta franja é eliminada.
Pelos cálculos anteriores, temos que as franjas eliminadas são dadas por:
Onde é a ordem da franja de interferência e é a ordem do mínimo de difração.
Com os nossos valores de e , temos:
Ou seja, máximos com ordem múltipla de quatro são cancelados da figura. Isso significa que o máximo com também não aparece na nossa figura de difração.
Com isso, a segunda maior ordem que aparece é .
Passo 5
Letra e)
A terceira maior ordem, pela discussão anterior, será .
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
Letra e)
Exercício Resolvido #13
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 141-49
Uma rede de difração com é iluminada com uma luz que contém apenas dois comprimentos de onda, e . O sinal incide perpendicularmente na rede.
- Qual é a distância angular entre os máximos de segunda ordem dos dois comprimentos de onda?
- Qual é o menor ângulo para o qual dois dos máximos se superpõem?
- Qual é a maior ordem para a qual máximos associados aos dois comprimentos de onda estão presentes na figura de difração?
Passo 1
Letra a)
Os máximos da figura de uma rede de difração são dados por:
O enunciado diz que:
- (máximos de segunda ordem)
Substituindo:
Logo, a distância angular entre os dois é:
Passo 2
Letra b)
Para dois máximos se sobreporem precisamos ter:
Os menores valores de e que satisfazem essa equação são e .
Nós usamos os menores pois, quanto menores eles forem, menor o ângulo do máximo. Esse ângulo vai ser:
Passo 3
Letra c)
Para encontrar os limites superiores das ordens dos máximos que aparecem na figura fazemos, para
E o maior máximo que aparece será o de ordem .
Para
E o maior máximo que aparece será o de ordem .
Resposta
Letra a)
Letra b)
Letra c)
A maior ordem para a qual máximos associados aos dois comprimentos de onda estão presentes na figura de difração é .
Exercício Resolvido #14
Halliday, Resnick, Jearl Walker, Fundamentos de física, volume 4: Óptica e Física Moderna, 8ª ed. Rio de Janeiro: LTC, 2009, pp 144-99
Uma rede de difração possui . Uma luz que contém todos os comprimentos de onda entre e incide perpendicularmente na rede.
- Qual é a menor ordem que se superpõe a outra ordem?
- Qual é a maior ordem para a qual o espectro completo está presente?
Passo 1
Letra a)
Para máximos de diferentes ordens (de diferentes comprimentos de onda) se sobreporem, seus ângulos precisam ser iguais.
No caso de redes de difração, os ângulos são dados por:
Para igualar os de dois comprimentos de onda:
Não está claro na questão, mas vamos considerar que os máximos são de ordens consecutivas. Assim:
Substituindo:
Quanto maior o valor de , menor a ordem necessária para sobrepormos. Assim, vamos usar:
No caso de , quanto menor o seu valor, menor o valor de . Assim, para acharmos um limite inferior para , podemos usar:
O resultado é:
Ou seja, a menor ordem possível para essa sobreposição ocorrer é .
A título de curiosidade, o comprimento de onda para que isso ocorra é:
Passo 2
Letra b)
Para acharmos a maior ordem para a qual o espectro completo está presente é necessário achar a maior ordem para a qual o maior comprimento de onda estará presente.
Isso é porque quanto maior o comprimento de onda, menos ordens estão presentes na figura.
Temos também:
Na rede de difração, o máximo é dado por:
Encontrando um limite superior para as ordens encontradas:
Ou seja, a maior ordem é .
Resposta
Letra a)
A maior ordem que se superpõe à ordem seguinte é .
Letra b)
A maior ordem para a qual o espectro completo está presente é .