A massa está uniformemente distribuída ao longo de um disco de raio . Determine o módulo, a direção e o sentido da força gravitacional entre o disco e a partícula de massa localizada a uma distância acima do centro do disco (Figura 12-39). O seu resultado se reduz a uma expressão correta quando assume valores muito elevados? (Sugestão: Divida o disco em anéis finos concêntricos infinitesimais; a seguir, integre o resultado para achar a força total.)
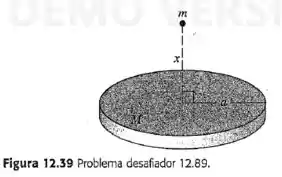
Passo 1
Beleza, esse problema é um pouco grandinho, mas vamos por partes que vai dar tudo certo.
Primeiramente vamos encontrar o campo gravitacional gerado por um anel fino de raio e massa . Desenhando vamos ter isso aqui:
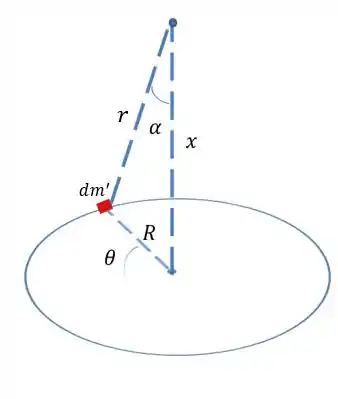
O que acontece é que pra cada pedacinho de massa do anel tem um outro pedacinho do outro lado e quando a gente soma a força gravitacional desses dois, a força resultante tem que apontar para baixo.
Isso significa que ao somarmos todas as contribuições de cada pedacinho do anel, a força total irá apontar para baixo também. Esse raciocínio é o que a gente chama de argumento de simetria!
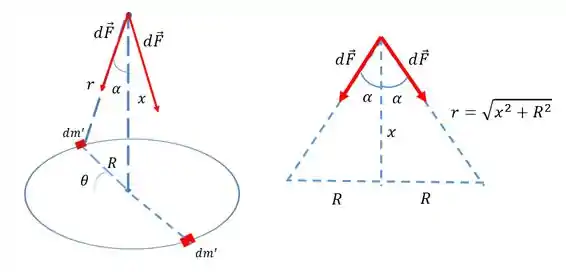
Como a nossa força resultante aponta para baixo, na hora de somar todas as contribuições vamos levar em consideração somente a componente vertical. Assim, olhando a geometria do nosso problema, pra projetar cada força na direção vertical a gente tem que multiplicar pelo cosseno de . Pela nossa figura
Passo 2
Outra coisa importante é que todos os pontos com massa desse anel estão à mesma distância r da massa , assim a força exercida por cada pedacinho vai ser
Mas como nos importa a componente vertical então temos que calcular
Aí agora temos que integrar esse cara pra calcular a força total
Nós vamos integrar todos os pedacinhos do anel agora, ou seja, só . Como , , e são os mesmos pra todos os pedaços então são constantes na nossa integral, o que permite que a gente faça
E o que é essa integral de ? É somente a massa total do nosso anel! Assim a força gravitacional exercida pelo anel será
Passo 3
Agora que já sabemos a força gravitacional para um anel genérico, temos que ajustar essa expressão encontrada para chegar na força exercida por um disco. Esse disco é composto por vários anéis e o raio desses anéis vai variar de até (raio do disco).
Pra isso então teremos que fazer uma nova integral que vai ser algo do tipo
Mas como ligar o anel com o disco? Bem, se eu disse que o que varia de um anel pro outro é o raio então temos que ter no final uma integral em !
Pra isso tem o pulo do gato que é olhar pra massa de cada anel! A densidade de massa de todos os anéis é igual, concorda? Eles são feitos do mesmo material! O que muda de um pro outro é o raio, e consequentemente o seu comprimento. Assim anéis maiores vão ter mais massa! Vamos usar essa informação então
Agora eu vou supor que um dado anel vai ter um raio e uma espessura beeeemm pequenina de forma que a sua área vai ser o seu comprimento vezes essa espessura
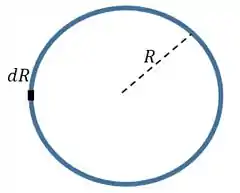
Qual vai ser a massa desse anel? Ela vai ser agora um
Esse é a densidade superficial de massa do disco! Se sabemos que o disco tem massa e área , então essa densidade superficial de massa é
Assim, a massa do anel será
No fundo nós fizemos essa regra de 3

Passo 4
Finalmente estamos prontos pra montar a nossa última (eu prometo!) integral
Já calculamos a força de anel um anel de massa
Como estamos falando de um anel de massa então vamos mudar para
Substituindo o do passo anterior
Jogando isso na nossa integral finalmente ficamos com
Finalmente temos uma integral com !!!!!!

Agora, vamos lá! Os limites de integração são de até e como a integral é em podemos tirar da integral tudo que é constante, assim
Passo 5
Agora é só fazer essa integralzinha aí rsrsrsrsrs
Você pode olhar no nosso material de cálculo onde tá tudo super explicadinho aqui! Eu vou fazer aqui, mas lá tem mais detalhes se você quiser dar uma relembrada, belezinha?
Essa integral é feita por substituição. Pra isso vamos definir uma nova variável pra sumir com esse do denominador, assim
De forma que (lembrando que é constante aqui!)
E os limites de integração ficam
Assim a nossa integral fica
Passo 6
Pronto! Agora é só jogar na nossa expressão da força!
Supondo , vamos ter , assim
Botando o fora do parênteses pra dentro
Show! Achamos a expressão pra força exercida pelo disco! Agora só falta botar a direção! Chamando de direção para baixo teremos
Passo 7
Agora vamos ver se essa expressão faz sentido quando assume valores muito elevados. O que significa isso? Isso significa tomar o limite de indo pra infinito! Pra isso vamos olhar a parte que contém na nossa expressão, ou seja, vamos olhar para o seguinte limite
Pra fazer esse cara vamos reescrever a raiz como
(Supondo )
Assim o nosso limite será
Então a nossa expressão pra força exercida pelo disco será
Ou seja, láááááá no infinito a força exercida pelo disco vai ser nula, o que faz total sentido já que quando a gente tiver infinitamente afastado de um corpo a influência dele será nula! ;)
Resposta
Essa expressão vai para no limite o que é o esperado quando dois corpos estão infinitamente afastados.