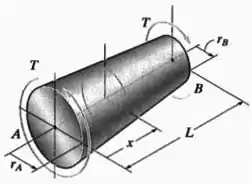
O eixo maciço tem conicidade linear de em uma extremidade e na outra extremidade. Deduza uma equação que dê a tensão de cisalhamento máxima no eixo em uma localização ao longo da linha central do eixo.
Dica do Expert: Se o seu professor/a sua professora não for do tipo que cobra:
- Exercícios literais;
- Ou exercícios com peças com formatos alternativos (como a peça desse exercício),
Sinta-se livre para pular para os próximos tópicos, que têm exercícios mais prováveis de cair em prova. 😉
Passo 1
O que está acontecendo?
Em uma seção qualquer do eixo, a tensão de cisalhamento máxima vai ser dada pela fórmula da torção:
Sendo que, em todas as seções, o torque vai ser o mesmo e o raio das seções vai variar entre e , dependendo da posição da seção que estiver sendo estudada.
Além disso, como o eixo é maciço, o seu momento polar de inércia vai ser dado pela fórmula:
E o que é que o exercício quer?
Ele quer que a gente encontre a tensão de cisalhamento máxima no eixo em uma certa seção de posição .
Então primeiro, temos que descrever o raio de uma seção em função de sua posição .
Em seguida, vamos substituir o que encontrarmos nas fórmulas da torção e do momento polar de inércia .
Assim, vamos encontrar a tensão de cisalhamento máxima em uma seção de posição no eixo!
Passo 2
Então vamos começar descrevendo o raio de uma seção em função de sua posição .
Para fazer isso, precisamos fazer um desenho observando como o raio das seções varia entre e ao longo do comprimento do eixo do exercício:
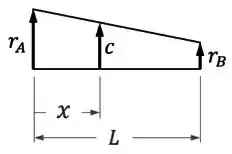
Quase sempre que temos uma variável que varia linearmente, como é o caso do nosso raio , uma das formas de descrever essa variável é fazendo uma semelhança de triângulos.
Então vamos tentar isso!
Os triângulos que existem nesse desenho são os triângulos que podem ser formados acima do raio :
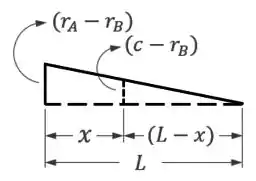
Aplicando a semelhança de triângulos entre:
- O triângulo menor, de base e altura ;
- E o triângulo maior, de base e altura ,
Temos que:
Passando os termos que estão dividindo para o outro lado, isso fica assim:
Em seguida, fazendo as distributivas, temos:
Cortando dos dois lados e colocando e em evidência, temos que:
Agora, como queremos definir o raio , devemos isolá-lo.
Fazendo isso, encontramos que:
Passo 3
Agora que já encontramos o raio de uma seção qualquer de posição , já podemos calcular a tensão de cisalhamento máxima nessa seção, que é o que o exercício quer!
Para tanto, aplicamos a fórmula da torção:
Substituímos a fórmula para o momento de inércia polar para um eixo maciço:
E simplificamos tudo, para encontrar que:
Agora, só falta substituir a expressão que encontramos para no passo anterior.
Fazendo isso, temos que:
Por fim, podemos deixar essa expressão mais bonita passando o para cima.
Fazendo isso, encontramos a nossa resposta final: