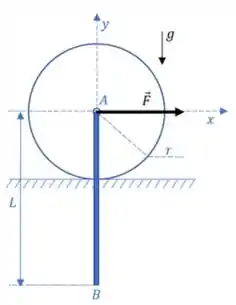
03) A figura mostra uma barra delgada AB de comprimento e massa articulada a um disco de raio e massa este último apoiado sobre uma pista horizontal áspera. O sistema parte do repouso sujeito a uma força horizontal aplicada ao centro A do disco. Sabendo que o disco rola sem escorregar, pede-se, para o instante da partida (instante imediatamente após a aplicação da força ):
a) Desenhar os diagramas de corpo livre do disco e da barra.
b) Escrever as equações do teorema da resultante e do teorema do momento da quantidade de movimento para o disco e para a barra.
c) Escrever as equações da cinemática pertinentes.
d) Determinar as acelerações angulares do disco e da barra.
Passo 1
Faaaaala galera do Responde Aí, como vocês estão? Animados pra matar mais uma questão de mecânica?
a) Nesse primeiro item precisamos apenas desenhar os diagramas de corpo livre (DCL) da barra AB e do disco.
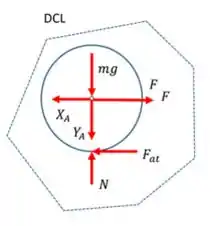
Começando pelo nosso disco, além da força temos também a força de atrito no contato com o solo, além do Peso e da Normal. Como no ponto A há uma articulação, devemos ter também reações e , nos eixos e , respectivamente. Supondo um sentido inicial para essas reações, podemos desenhar:
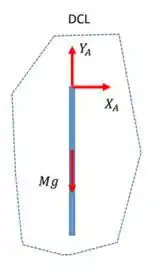
Agora para a barra AB, temos também as reações da articulação, mas agora em sentidos opostos ao do disco. Além disso, também atua a força peso no CM da barra, que pela simetria fica no seu centro. Assim:
Passo 2
b) Continuando, agora precisamos escrever as equações do Teorema da Resultante e do Teorema do Momento da Quantidade de Movimento (TQMA) tanto para o disco, como para a barra.
Começando pelo disco, e lembrando que o teorema da resultante é basicamente uma 2° lei de Newton quando a massa do corpo é constante, temos:
(1)
Agora pelo TQMA, vem que:
A única força que faz momento em A é o atrito, logo:
Indo agora para a barra AB, temos:
(3)
Já pelo TQMA, temos:
Mas a única força que faz momento em G é , daí:
Prontinho 😊
Passo 3
c) Nesse item o enunciado nos pede para escrever as equações cinemáticas pertinentes. Mas o que seria pertinente né? No caso, são aquelas equações que vão ser úteis pra gente resolver o problema. Pelas equações do item anterior e os teoremas usados, sabemos que vamos precisar relacionar a aceleração linear da barra e do disco com suas acelerações angular.
Então, para o ponto A que está apenas transladando, podemos escrever que:
Já para o ponto G, ele tanto rotaciona como translada, então se encaixa em um movimento plano geral. Daí podemos escrever:
Nesse ponto tem uma sacada bem importante. Como o instante considerado pelo enunciado é imediatamente após a aplicação da força , e o sistema parte do repouso, temos que:
Assim, reescrevendo ficamos com:
Passo 4
d) Beleza, finalmente chegamos no ápice da nossa questão. Precisamos encontrar as acelerações angulares do disco e da barra. Bora reescrever as equações que já encontramos até aqui pra ver se já conseguimos finalizar a questão.
De (2) e de (4) também podemos escrever que:
Massa! Agora podemos visualizar melhor como atacar esse sistema. Uma boa ideia é substituir (9) e (10) em (5) e (7). Daí, em (7):
Agora em (5):
E, por fim:
Aeeee, terminamos!! Essa questão era bem complicadinha, mas conseguimos matar ela também. Espero que vocês tenham entendido bem, até a próxima pessoal 😉
Resposta
a) Resolução no texto.
b) Resolução no texto.
c) Resolução no texto.
d)