Determine a solução da inequação para
Passo 1
A primeira coisa que vamos fazer é abrir esse produto notável e melhorar a cara dessa inequação:
Rearrumando, temos:
Lembra da relação fundamental da trigonometria?
Ela nos diz que:
Substituindo, teremos:
Por fim, podemos escrever:
Essa expressão é bem mais amigável, né?
Passo 2
Show, agora precisamos analisar algumas coisas...
Só de olhar, percebemos que nem o seno e nem o cosseno podem ser iguais a zero. Mas para quais valores de x vai valer essa nossa inequação?
Vamos analisar o nosso ciclo trigonométrico:
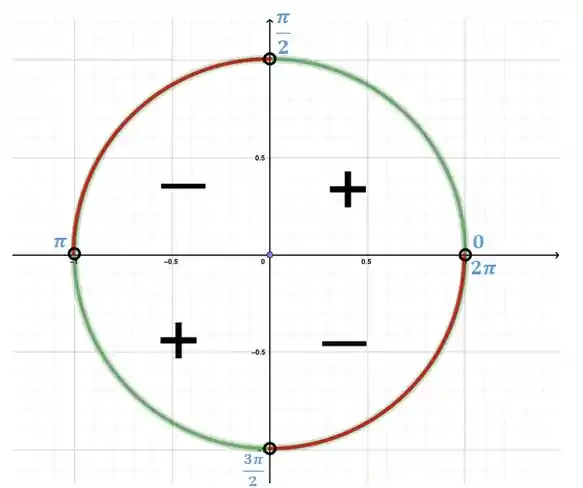
Os únicos intervalos onde teremos essa multiplicação dando valores negativos, vai ser entre e entre
Ou seja nossa solucão será: