Determine a solução da inequação para
Passo 1
Ora ora, espere um pouco! Ainda não vimos nada parecido com isso, certo?
Não precisa se desesperar, se você observar direitinho essa estrutura parece uma inequação do 2º grau, né?
Para isso acontecer, basta dizermos que:
Aí, nossa inequação vai ficar com essa cara aqui:
Agora sim, isso a gente sabe resolver! (Ou pelo menos deveria hahaha)
Passo 2
Show, vamos resolver essa nova inequação que encontramos:
Aplicando Bhaskara na equação, teremos:
Então:
Passo 3
Como a função é crescente, então teremos algo assim para o nosso gráfico:
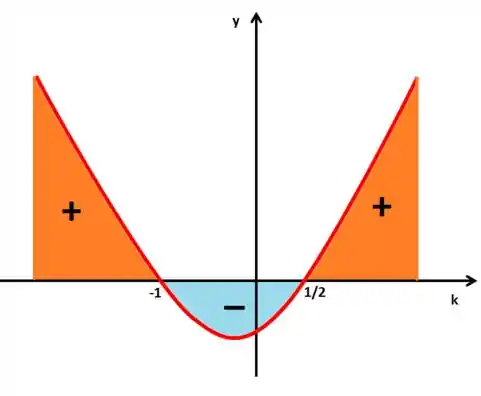
Ou seja, o y só será positivo para:
Passo 4
Mas espera um pouco, lá no início a gente disse que
Então, teremos que:
Já vimos que o cosx está sempre entre -1 e 1, então não é possível ele ser menor que -1 em nenhum intervalo.
Para o intervalo que foi proposto no enunciado( teremos:
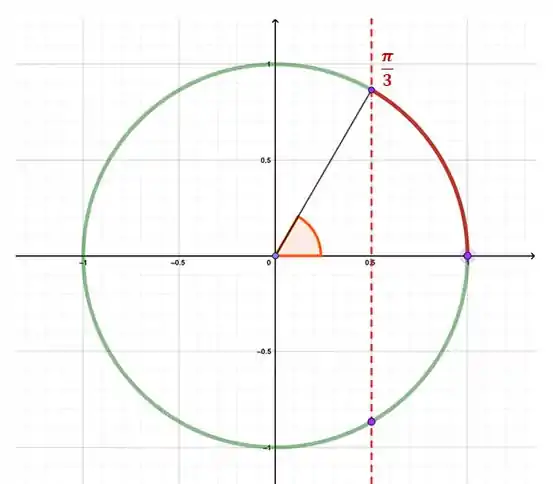
Queremos todos os à direita dessa reta e que estejam no intervalo do enunciado, ou seja:
Show?