Uma película muito fina de material transparente, de índice de refração é utilizada como revestimento antirrefletor na superfície de um vidro de índice de refração de uma célula solar. Qual deve ser a espessura mínima da película para uma incidência perpendicular não ser observar por reflexão da luz que no vácuo tem comprimento de onda ?
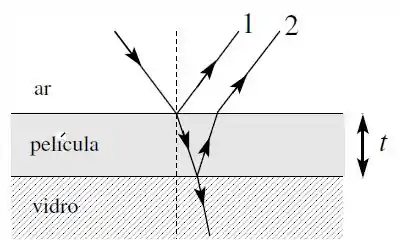
Passo 1
Primeiro, devemos saber a diferença de caminho ótico entre os feixes e . Para tanto, considere a figura abaixo.
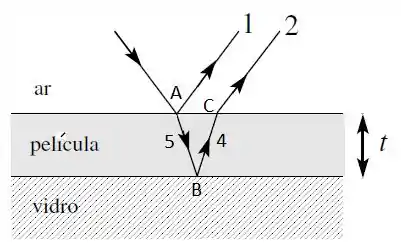
Um observador verá os feixes e vindo dos pontos e . Assim, a diferença de caminho ótico entre os feixes e é a distância que um feixe percorreu a mais (ou a menos) que o outro feixe.
Notamos primeiramente que para formar o feixe 2, antes o feixe passou pelos pontos e (feixes e ). Assim, a diferença de caminho é exatamente a soma dos percursos os feixes e fizeram.
Como a incidência é quase normal, então o feixe percorreu a espessura da película até o ponto , enquanto que o feixe 4 também percorreu a espessura da película até o ponto . Assim, temos que a diferença de caminho ótico é
Agora, vamos ver o que precisamos para não ser observado a reflexão dos feixes e .
Passo 2
Para não haver a reflexão da luz, os feixes 1 e 2 devem interferir destrutivamente. Isto significa que a diferença entre o caminho ótico dos feixes 1 e 2 deve ser igual um múltiplo ímpar de metade do comprimento de onda da luz dentro da película. Deste modo, temos que
No entanto, antes de usar a expressão acima, devemos saber se os feixes refletidos mudaram de fase ou não. Veremos no próximo passo como verificar isso.
Passo 3
Para sabermos se as fases dos feixes refletido mudaram, existe uma regrinha bem legal que podemos aplicar. A regra é
Assim, vamos analisar o feixe 1. Sabemos que ele provém de uma reflexão de um feixe que vai do ar para a película ( e ). Logo, , então o feixe 1 mudou de fase de um valor Vamos analisar agora o feixe 2. Sabemos que ele provém de uma reflexão de um feixe que vai da película para o vidro ( e ). Logo, , então o feixe 2 também mudou de fase de um valor Ih! Deu ruim! Os dois feixes mudaram de fase! E agora?Vamos entender o que significa mudar de fase. Mudar de um valor significa que na verdade o feixe está invertido. Igual a quando balançamos uma corda presa em uma das extremidades. A onda refletida é invertida.
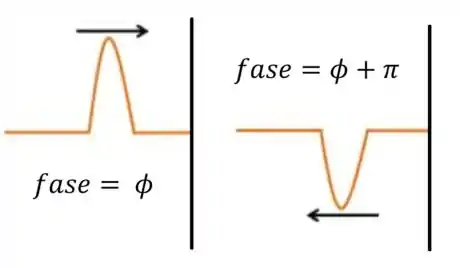
Mas aí que vem o pulo do gato. Quando um feixe está invertido, podemos dizer que é igual ao feixe original atrasado de .
Desta forma, podemos dizer que ambos os feixes estão atrasados de ! Ora, mas isso é a mesma coisa que se não tivessem!Portanto, a equação para interferência destrutiva, agora considerando a fase dos feixes refletidos é
Passo 4
Até agora, tratamos com o comprimento de onda da luz dentro da película (). Podemos relacionar com o comprimento de onda no vácuo () a partir da expressão abaixo.
Assim, temos que a condição para interferência destrutiva se torna
A menor espessura para a película equivale a tomarmos . Assim,
Substituindo os valores de e dados no enunciado, temos finalmente que