Com base no conjunto de pontos abaixo, resolva a interpolação inversa usando a segunda abordagem de resolução do capítulo utilizando a inversão de termos e compare com a resolução do exercício anterior. Escolha o método que achar necessário para a resolução do polinômio. Além disso, encontre se :

Passo 1
Antes de iniciar a resolução do problema, vale atentar que estamos usando calculadoras diferentes e arredondamentos diferentes, o que pode acarretar pequenas divergências no resultado final, mas se chegar próximo ao que calculamos aqui já está bem aceitável!!!
O primeiro passo para resolver esse exercício é inverter as colunas, tudo aquilo que é passa a ser :
![]()
Agora, ficamos com :
Passo 2
Com base nesse conjunto de pontos, podemos montar a tabela de diferenças divididas e montar o polinômio interpolador, utilizando o método de Newton:
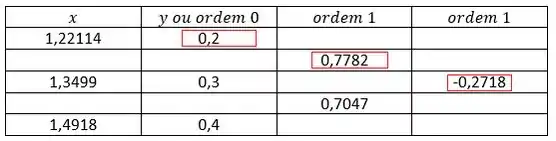
Com esses valores grifados, podemos montar o polinômio interpolador de ordem 2 em função de :
Se:
Se :
Quando o valor de
Passo 3
Comparando com a resolução do método anterior, essa maneira se torna menos trabalhosa e fornece o resultado correto com menos esforço, apesar da diferença de 0,0002 entre eles.
Resposta
o valor de