Estabeleça o sistema de equações dado abaixo a partir da figura.
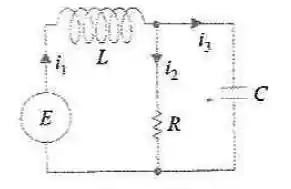
Passo 1
Nessa questão vamos ter que usar os conhecimentos de física para montar as equações. Sabemos da primeira lei de Kirchhoff que
Para acharmos as outras equações vamos ter que analisar cada malha separada.
Passo 2
Analisando somente a malha que contem o indutor e o resistor . Pela segunda lei de Kirchhoff temos.
Já encontramos nossa primeira equação.
Passo 3
Analisando a malha geral. Pela segunda lei de Kirchhoff temos.
Como é a carga que está no capacitor e é a única corrente que passa pelo capacitor, temos.
Passo 4
Ao igualarmos as equações encontradas no passo 2 e 3.
Como nós sabemos que
Como sabemos que
Encontramos nossa segunda equação.
Resposta
Demonstramos como encontrar as equações a partir da figura.
Exercícios de Livros Relacionados
Transforme o sistema: m 1 d 2 x 1 d t 2 = k 2 x 2 - x 1 - k 1 x 1 + F 1 t ; m 2 d 2 x 2 d t 2 = - k 3 x 2 - k 2 x 2 - x 1 + F 2 t Em um sistema de primeira ordem fazendo y 1 = x 1 , y 2 = x 2 , y 3 =
As equações: m 1 d 2 x 1 d t 2 = k 2 x 2 - x 1 - k 1 x 1 + F 1 t ; m 2 d 2 x 2 d t 2 = - k 3 x 2 - k 2 x 2 - x 1 + F 2 t Podem ser deduzidas desenhando-se um diagrama de forças agindo sobre cada massa
Considere o circuito ilustrado na figura a seguir.Sejam I 1 , I 2 e I 3 as correntes atravessando, respectivamente, o capacitor, a resistência e o indutor. Analogamente, sejam V 1 , V 2 e V 3 as difer
Considere dois tanques interligados de maneira análoga aos da figura a seguir. O tanque 1 contém, inicialmente, 60 gal de água e Q 1 0 oz de sal, enquanto o tanque 2 contém, inicialmente, 100 gal de á
Considere os dois tanques interligados na figura a seguir. O tanque 1 contém, inicialmente, 30 gal de água e 25 oz de sal, enquanto o tanque 2 contém, inicialmente, 20 gal de água e 15 oz de sal. Entr