Exercício nº 1 letra lista 6 de Cálculo III – IME - UERJ – Prof. Fernando Lopes C. -2014
Resolva o sistema de oscilações
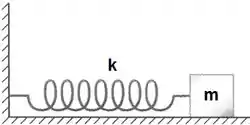
Passo 1
Vamos usar a segunda lei de Newton para conseguir montar a equação diferencial.
Mas para isso, precisamos fazer o diagrama de forças.
Analisando as forças atuantes no bloco em um instante genérico temos:
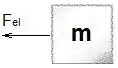
Só temos a força elástica (normal e peso se anulam). Logo, a força resultante é a força elástica.
Passo 2
Então, pelo diagrama de forças atuantes temos:
Porém, pela Lei de Hooke:
Logo:
Substituindo na Segunda Lei de Newton:
Que é o mesmo que:
Onde:
Passo 3
A equação característica dessa EDO é:
Logo
O que evidencia que a solução tem a carona de:
Da pra juntar esses dois caras em um só:
E tchã!Fechou clã! Isso vale para o pêndulo físico e o pêndulo simples! O que muda em cada um deles é o !