Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento de Inércia e Raio de Rotação de Regiões Planas

Ver Teoria
Exercício 5123467891011121314

Enunciado

Encontre os raios de rotação em relação aos eixos coordenados e o raio de rotação polar de uma placa fina triangular limitada pelas retas y = x , y = - x e y = 1 se δ x , y = y + 1

Passo 1

Sabemos que a fórmula dos raios de rotação são as seguintes:

R x = I x M

R y = I y M

R 0 = I 0 M

Portanto vamos precisar calcular três integrais duplas! Dois momentos de inércia e uma para a massa total! I 0 podemos obter a partir da soma de I x e I y .

Vamos então descrever os limites da nossa região D , calcular os momentos de inércia e a massa e depois só jogar na fórmula do raio. Vamos lá?

Passo 2

O gráfico da nossa região triangular é esse aqui:

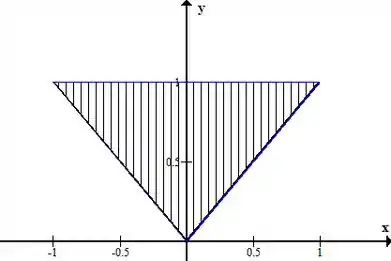
Escolhendo os limites de integração pelo tipo II:

- y ≤ x ≤ y

0 ≤ y ≤ 1

Passo 3

Para calcular o momento de inércia em relação ao eixo x usamos a integral:

I x = ∬ D y 2 δ x , y d A = ∫ 0 1 ∫ - y y y 2 y + 1 d x d y

= ∫ 0 1 ∫ - y y y 3 + y 2 d x d y

∫ 0 1 [ x y 3 + y 2 ] x = - y x = y d y

= ∫ 0 1 y - - y y 3 + y 2 d y = ∫ 0 1 2 y 4 + 2 y 3 d y

= 2 y 5 5 + 2 y 4 4 y = 0 y = 1 = 2 5 + 2 4 = 9 10

I x = 9 10

Passo 4

Para calcular o momento de inércia em relação ao eixo y usamos a integral:

I y = ∬ D x 2 δ x , y d A = ∫ 0 1 ∫ - y y x 2 y + 1 d x d y

= ∫ 0 1 x 3 3 x = - y x = y y + 1 d y

= ∫ 0 1 y 3 - - y 3 3 y + 1 d y = ∫ 0 1 2 y 3 3 y + 1 d y  

= 2 3 ∫ 0 1 y 4 + y 3 d y

= 2 3 y 5 5 + y 4 4 y = 0 y = 1 = 2 3 1 5 + 1 4 = 2 3 9 20 = 3 10

I y = 3 10

Sabendo que I x e I y podemos calcular I 0 :

I 0 = I x + I y = 3 10 + 9 10 = 12 10 = 6 5

I 0 = 6 5

Passo 5

Para calcular a massa M vamos usar a integral:

M = ∬ D δ x , y d A = ∫ 0 1 ∫ - y y ( y + 1 ) d x d y

= ∫ 0 1 y - - y y + 1 d y = ∫ 0 1 2 y ( y + 1 ) d y

= 2 ∫ 0 1 y 2 + y   d y

= 2 y 3 3 + y 2 2 y = 0 y = 1 = 2 1 3 + 1 2 = 2 5 6 = 5 3

M = 5 3

Passo 6

Agora é só jogar tudo nas fórmulas dos raios de rotação!

R x = I x M = 9 10 5 3 = 27 50 = 3 6 10

R y = I 0 M = 3 10 5 3 = 9 50 = 3 2 10

R 0 = I 0 M = 6 5 5 3 = 18 25 = 3 2 5

Resposta

R x = 3 6 10

R y = 3 2 10

R 0 = 3 2 5

Exercícios de Livros Relacionados

Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for ρ x ,y = 1 + 0,1 x , é mais difícil girar a pá em tor
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D = x , y 0 ≤ y ≤ x e - x ,0 ≤ x ≤
Calcular o momento de inércia em relação ao eixo dos x de uma chapa delimitada por x + y = 4 ,x = 4ey = 4 . Considerar a densidade igual a uma constante igual a k
Calcular o momento de inércia de uma quadrado de lado igual a 4 cm em relação ao eixo que passa por uma diagonal. Considerar a densidade constante.
Calcular o momento de inércia de um disco circular de diâmetro 10 cm:a) Em relação ao seu próprio centrob) em relação ao seu diâmetro Considerara densidade igual uma constante K