A barra gira uniformemente em torno do pino , com velocidade angular constante . Determine a velocidade e a aceleração do bloco , no instante em que .
Dados: ; .
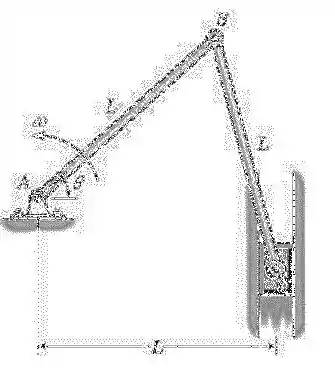
Passo 1
O que temos que fazer nesses tipos de questões é achar uma relação trigonométrica entre o que queremos saber e o que temos de informação. A questão quer saber o movimento de quando :
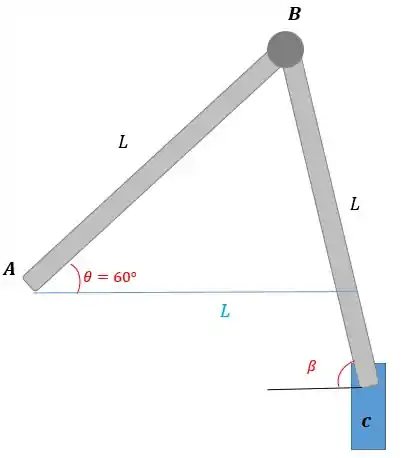
Temos que o comprimento da base pode ser escrito como:
Dividindo toda nossa equação por , temos:
Sabemos que , então:
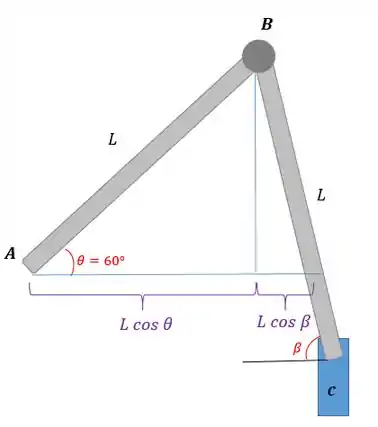
Passo 2
Nós temos a seguinte relação:
Agora vamos derivar isso, para relacionar as velocidades angulares de e :
Sabemos que:
Como e , então:
Passo 3
Vamos derivar a equação que achamos no passo anterior para acharmos uma relação entre as acelerações angulares:
Para derivar isso temos que usar a regra da cadeia e a regra do produto e vamos ficar com:
Repare que a velocidade angular da barra é constante, então a sua velocidade angular será zero:
Vamos substituir o que temos:
Passo 4
Agora vamos achar uma equação que relacione o deslocamento vertical do bloco :
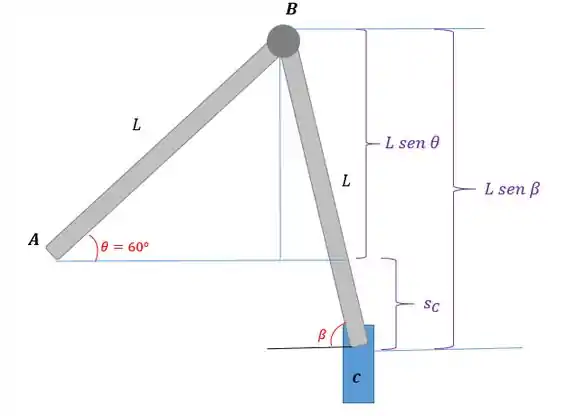
Repare que o deslocamento vertical do ponto será:
Sabemos que , e , então:
Ou seja, não teve deslocamento vertical.
Passo 5
Agora vamos derivar essa equação que achamos para achar uma equação para a velocidade de :
Substituindo o que temos:
Passo 6
Para acharmos a aceleração do bloco , temos que derivar a equação da velocidade que acabamos de encontrar:
Vamos ter que:
Substituindo os valores que já temos: