Tipos de Erros Estatísticos
Teoria
Fala aí! Seja muito bem vindo ao Responde Aí! Bora conversar um pouco sobre os tipos de erros estatísticos?!
Mas antes de qualquer coisa, vamos relembrar o que são os testes de hipóteses! 👇
Teste de Hipóteses
Em um teste de hipóteses definimos uma hipótese nula
A média dos alunos que estudam probabilidade e estatística pelo Responde Aí é igual a
Para fazer um teste de hipóteses a gente pode dizer que:
O próximo passo é analisar os parâmetros pra decidir se podemos ou não rejeitar a hipótese nula. Mas…e se a gente errar? E se a hipótese nula for verdadeira e a gente rejeitar ela? E se for ao contrário, se a média dos alunos que estudam pelo RA for 8.5 e mesmo assim a gente aceitar a hipótese nula?!
Qual é a probabilidade de aceitarmos ou rejeitarmos a hipótese nula erroneamente?! É isso que a gente vai descobrir agora!
Erro do Tipo 1: Rejeitar a Hipótese Nula Erroneamente
O erro do tipo 1 acontece quando a hipótese nula esta correta mas mesmo assim ela é rejeitada! Pra ficar mais claro, vamos fazer um exemplo:
Uma indústria compra ímãs importados, que devem satisfazer algumas exigências quanto a resistência à tração dos mesmos. Compramos majoritariamente de dois países (A e B) que possuem diferenças entre si.
- País A:
- Resistência Média à tração:
- Desvio-padrão:
- Resistência Média à tração:
- País B:
- Resistência Média à tração:
- Desvio-padrão:
- Resistência Média à tração:
Um lote será leiloado e a empresa precisa saber qual país de origem antes de fazer uma oferta. Uma amostra de 25 unidades é coletada. Pouco antes do leilão será divulgada a média amostral,
Bom, primeiro de tudo, montamos nossas hipóteses assim:
- Hipótese Nula
: Os ímãs são de origem B - Hipótese Alternativa
: Os ímãs são de origem B
Considerando a região crítica:
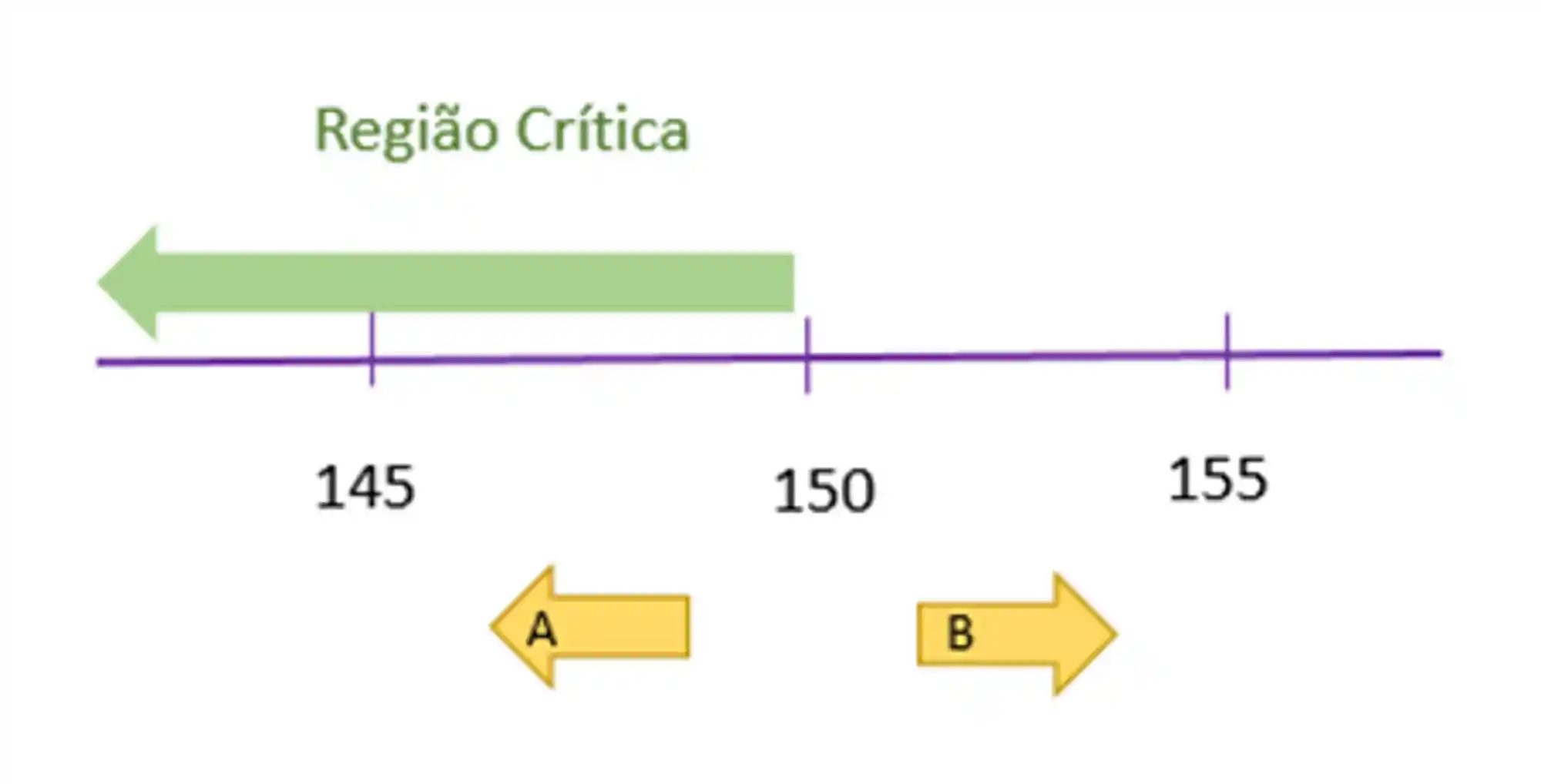
Podemos definir as probabilidades de erro do tipo
Lembrando que, pra um caso geral temos:
Você também pode conferir esse conteúdo em vídeo!
Para calcular a probabilidade do erro
Ou seja, se
Onde
Para que nossa média amostral
Padronizando, temos:
Pela tabela normal, temos que:
A probabilidade de ser
Erro do Tipo 2: Aceitar a Hipótese Nula Erroneamente
O erro do tipo 2 acontece quando a hipótese alternativa esta correta mas mesmo assim a gente aceita a hipótese nula. Para calcular a probabilidade do erro do tipo
O passo a passo é igual o que vimos acima:
Padronizando, temos:
Pela tabela normal temos que:
Logo, a probabilidade de dizermos que é de
Ou pra um caso geral:
Se rejeitarmos
Erro do Tipo 2: Aceitar a Hipótese Nula Erroneamente
Exercícios Resolvidos
Exercício Resolvido #1
Morettin & Bussab, Estatística Básica 5ª edição, pág 329
Para decidirmos se os habitantes de uma ilha são descendentes da civilização A ou B, iremos proceder do seguinte modo:
- Selecionamos uma amostra de 100 moradores adultos da ilha, e determinamos a altura média deles;
- Se essa altura média for superior a 176, diremos que são descendentes de B; caso contrário, são descendentes de A.
Os parâmetros das alturas das duas civilizações são:
Qual a probabilidade do erro de tipo I? E do erro de tipo II?
Passo 1
Primeiro vamos definir nossas hipóteses:
Note que aqui você poderia definir o contrário se quisesse.
Sabendo disso, nossa região crítica vai ser quando:
Que é quando rejeitamos a hipótese nula.
Passo 2
Então a probabilidade do erro de tipo vai ser:
Padronizando isso aí:
Procurando esse na tabela vemos que...
Então:
Passo 3
Padronizando:
Então vai dar no mesmo cálculo que fizemos para o erro :
Então:
Resposta
Exercício Resolvido #2
Morettin & Bussab, Estatística Básica 5ª edição, pág 329
Para decidirmos se os habitantes de uma ilha são descendentes da civilização A ou B, iremos proceder do seguinte modo:
- Selecionamos uma amostra de 100 moradores adultos da ilha, e determinamos a altura média deles;
- Se essa altura média for superior a 176, diremos que são descendentes de B; caso contrário, são descendentes de A.
Os parâmetros das alturas das duas civilizações são:
Qual deve ser a regra de decisão se quisermos fixar a probabilidade do erro de tipo em 5%? Qual a probabilidade do erro de tipo , nesse caso?
Passo 1
A questão tá perguntando a regra de decisão que devemos adotar, ou seja, qual deve ser o valor crítico do nosso teste, que vai dividir nossas regiões entre crítica e de aceitação. Basicamente queremos ignorar o ponto dado no item ii) e descobrir qual o novo valor desse ponto.
E a regra de decisão deve garantir que o erro de tipo valha , ou seja:
Padronizando isso aí:
Invertendo o sinal:
Se tentarmos procurar o no corpo da tabela da Normal, vamos perceber que algumas tabelas não tem esse valor. Nesse caso, procuramos o complementar de , ou seja, e colocamos o sinal de negativo na frente:
Onde:
Então:
Passo 2
Então agora o erro de tipo fica:
Padronizando:
Resposta
Exercício Resolvido #3
Elaboração Própria
Seja o Q.I. dos estudantes de certa escola, com distribuição Normal de média desconhecida e desvio padrão 15. Suponha que se uma média amostral do Q.I. dos estudantes for maior que , eles são considerados acima da média. Foi retirada uma amostra aleatória de 25 estudantes cujo Q.I. médio foi 106.
Calcule a probabilidade de cometer um erro de tipo (), tomando como valor crítico para a média e considerando que o verdadeiro valor da média dos Q.I. de todos os alunos da escola é .
Passo 1
Definindo as hipóteses:
Passo 2
A probabilidade do erro de tipo II acontecer é dada por:
Padronizando:
Resposta
Exercício Resolvido #4
Elaboração Própria
Calcule o ponto crítico de um teste que quer averiguar se a quantidade média de creme de leite em latinhas é inferior . Para a realização do teste, foram analisadas 12 latinhas e obtida uma média de . Considere o desvio padrão igual a e .
Passo 1
Primeiramente vamos escrever as hipóteses do nosso teste:
Já que queremos averiguar se a quantidade média é menor que !
Passo 2
Como estamos num teste unilateral inferior, nossa ponto crítico é dado por:
E a nossa estatística de teste para média é:
Igualando esses dois caras:
Lembrando que é o ponto crítico!
Passo 3
Agora podemos substituir os valores do enunciado:
Resposta
Exercício Resolvido #5
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006,330-03
Nas situações abaixo, escolha como hipótese nula aquela que para você leva a um erro do tipo I mais importante. Descobre quais dos dois erros em cada caso.
a) O trabalho de um operador de radar é detectar aeronaves inimigas. Quando surge alguma coisa estranha na tela, ele deve decidir entre as hipóteses:
1. Está tendo um ataque
2. tudo bem, apenas uma leve interferência.
b) Um pesquisador acredita que descobriu uma vacina contra resfriado. Ele irá conduzir uma pesquisa de laboratório para verificar a veracidade da afirmação. De acordo com o resultado, ele lançará ou não a vacina no mercado. As hipóteses que pode testar são:
1. a vacina é eficaz;
2. a vacina não é eficaz.
Passo 1
Vamos analisar a letra a)
O trabalho do operador é detectar aeronaves inimigas, portanto o erro é rejeitar a afirmação de um ataque, quando o mesmo está ocorrendo é gravíssima. Assim,
Está tendo um ataque
Rejeitar , o fato de estar tendo um ataque, quando o mesmo é verdadeiro.
tudo bem, apenas uma leve interferência
Aceitar quando a mesma é falsa
Passo 2
Analisando a letra b)
Mesmo que não exista nenhum efeito colateral é pior distribuir algo que não ajuda em nada, ou seja, nossa hipótese deve ser que a a vacina não é eficaz.
A vacina não é eficaz
dizendo que a vacina é eficaz, quando é verdadeira, ou seja, quando ela não é.
A vacina é eficaz.
Aceitar quando a mesma é falsa
Resposta
Ei, a resposta está no passo a passo :)