Função de distribuição acumulada
Teoria
A FDA – Função de Distribuição Acumulada de uma variável aleatória é uma função
Quando estamos tratando de variáveis aleatórias discretas a Função de Distribuição Acumulada é dada por:
E quando tratamos de variáveis aleatórias contínuas a Função de Distribuição Acumulada é dada por:
Meio confuso né? Mas não se preocupe, vamos ver um exemplo que vai esclarecer tudo.
Exemplo:
O tempo de vida útil de um equipamento eletrônico de determinado tipo pode ser expresso por uma v.a. contínua
Qual a Função de Distribuição Acumulada do tempo de vida útil do equipamento?
Passo 1
Para começar, sabemos que se
Já que, para
Passo 2
Agora vamos pensar no caso de
Podemos quebrar essa integral em duas partes, uma que vai de menos infinito até 0, e uma segunda que vai de zero até
Agora vamos substituir a expressão
Ou seja:
Passo 3
Agora que já consideramos os dois casos, podemos definir a nossa Função de distribuição acumulada como:
E prontinho! Bem de boas!
Gráfico de uma Função de Distribuição Acumulada
Quando tratamos de variáveis aleatórias contínuas o gráfico das Funções de Distribuição Acumulada terão a carinha de um degrau:
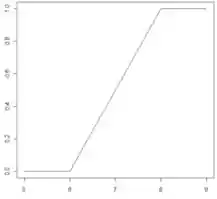
Os gráficos de FDA de variáveis contínuas sempre têm três características:
- A curva é sempre contínua e crescente
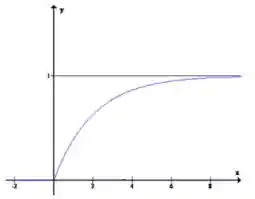
Por exemplo, vamos esboçar o gráfico da FDA do exemplo anterior.
Se quiséssemos descobrir o valor de
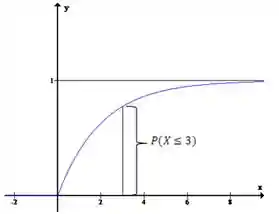
Fazendo as continhas, teremos
Massa demais, não é?!
Então, continua aqui no Responde Aí com esse vídeo maneiro sobre FDA.
Exemplo:
Gráfico de uma Função de Distribuição Acumulada
Exercícios Resolvidos
Exercício Resolvido #1
PUCRIO-P1-2012.1-4
A renda de uma pessoa numa população é uma variável aleatória contínua com densidade , apenas para .
- Ache a constante que faz uma densidade.
- Encontre a função de distribuição acumulada de .
- Calcule a mediana da distribuição de .
Passo 1
(a)
Mais uma vez, calcular essas constantes. Muito tranquilo, pra uma v.a. contínua, é só integrar a função em todo seu domínio que o resultado tem que ser .
Isso tem que ser igual a .
Passo 2
(b)
Função de distribuição acumulada para , vai ser , já que só é definido a partir de zero.
Para , a FDA será , porque já terá acumulado todo o domínio da função, então tem que ser .
Para o intervalo de definição de , a gente integra...
Temos então:
Passo 3
(c)
A mediana é o valor que divide a distribuição no meio, ou seja, dos valores estão abaixo dele e o resto acima.
Pra descobrir a mediana é só a gente usar a nossa e igualar ela a , aí encontraremos o valor do .
Passo 4
Vamos resolver essa equação e achar as raízes.
Temos duas raízes possíveis.
Só que a primeira raiz é maior do que , ou seja, tá fora do intervalo e não serve pra gente.
Com isso, nossa resposta final será:
Já que esse valor está dentro do intervalo .
Resposta
Exercício Resolvido #2
UFF – Departamento de Estatística, Apostila profª Ana Maria Lima de Farias
A função de densidade de uma variável aleatória é dada pela função cujo gráfico se encontra na figura:
e) Calcule a função de distribuição acumulada e esboce seu gráfico.
Passo 1
Nós sabemos que a FDA é a integral da função de densidade de menos infinito até , certo? Então vamos ter que descobrir primeiro a equação da função de densidade .
Mas olhando o gráfico dela, vemos que é uma reta! E toda reta tem o formato . Para descobrir o valor das constantes e , vamos usar nossos pontos conhecidos no gráfico:
Isso dá pra gente:
Resolvendo esse sisteminha, achamos que e .
Então nossa função de densidade é:
Mas repara que no gráfico essa reta só tá desenhada para os pontos onde , certo? Então esse é o intervalo que nossa função de densidade existe. Para pontos fora desse intervalo, ela vai valer zero.
Passo 2
Agora vamos lembrar a fórmula da FDA:
Onde esse é simplesmente a com reescrito no lugar do , só pra gente não confundir com o do limite de integração. Então:
Uééé, mas por que começou em zero? Porque antes disso nossa função de densidade era zero, ora bolas! Então não vai mudar nada no cálculo começar daí. Integrando temos:
Então a FDA é:
Mas isso aí é só para , certo? Por que é esse intervalo que a função de densidade existe. A expressão completa fica:
Por que na FDA é sempre se estamos antes de existir () e se estamos depois ().
Passo 3
Socorro mas e o gráfico disso? Isso aí é uma equação de 2º grau, gente! Ou seja, é uma parábola! Como a constante que tá multiplicando o é negativa, vai ser uma parábola com a concavidade para baixo.
E a FDA sempre começa com e termina em , certo? Desenhando uma parábola com concavidade para baixo seguindo essas condições, teríamos isso aqui:
Resposta
Exercício Resolvido #3
Elaboração Própria
O diâmetro de um cabo elétrico é uma variável aleatória contínua com função de densidade dada por
Usando a função de distribuição acumulada, determine a probabilidade do diâmetro ser maior que .
Passo 1
Primeiro calculamos nossa FDA por:
Então:
Passo 2
Nós sabemos que a FDA representa o valor de todas as probabilidades até certo , correto? Tipo assim:
E o que é pedido para a gente é a probabilidade do diâmetro ser maior que , ou seja:
Mas usando a probabilidade complementar, sabemos que:
Opa! E é uma FDA, certo? Então:
Então a probabilidade que queremos...