Exercícios de Função de Distribuição Acumulada para V.A. Contínua - Lista de Exercícios Resolvida
Questão 1
A renda de uma pessoa numa população é uma variável aleatória contínua com densidade , apenas para .
- Ache a constante que faz uma densidade.
- Encontre a função de distribuição acumulada de .
- Calcule a mediana da distribuição de .
Questão 2
O diâmetro de um cabo elétrico é uma variável aleatória contínua com função de densidade dada por
Usando a função de distribuição acumulada, determine a probabilidade do diâmetro ser maior que .
Ver solução completaQuestão 3
A função de densidade de uma variável aleatória é dada pela função cujo gráfico se encontra na figura:
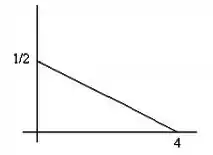
e) Calcule a função de distribuição acumulada e esboce seu gráfico.
Ver solução completaQuestão 4
Admita que o atendimento, em minutos, num caixa de um banco seja uma variável aleatória , com densidade
a) Mostre que, de fato, é uma função de densidade.
b) Calcule a função de distribuição acumulada do tempo de atendimento, . Calcule também .
c) Suponha agora que o tempo de atendimento do outro caixa, , seja uma variável aleatória com densidade
Calcule e .
Ver solução completaQuestão 5
Uma variável aleatória contínua tem a seguinte função de densidade de probabilidade:
a) Encontre a função de distribuição de probabilidade acumulada de .
b) Calcule e .
c) Calcule a média de .
Ver solução completaQuestão 6
Seja uma variável aleatória que toma valores no conjunto é a sua função de distribuição (acumulada). Considere as afirmações abaixo.
a) é uma variável aleatória contínua.
b) é uma função estritamente crescente.
c) Para todo ∈ R, existe o limite e vale .
As afirmações verdadeiras são:
Ver solução completaQuestão 7
12) O tempo que um aparelho eletrônico funciona sem apresentar defeito tem distribuição exponencial com média . Este não apresentou defeito até o momento, mas não se sabe por quanto tempo já foi usado. Qual a probabilidade de que não apresente defeito durante as próximas ?
a) .
b) é necessário saber .
c) .
d) .
e) .
Ver solução completa