Calcule o comprimento de onda da radiação emitida por um átomo de hidrogênio para e . Identifique a linha espectral no espectro do hidrogênio abaixo.
Passo 1
Se ele dá os valores de e e pede o comprimento de onda, vamos usar essa equação aqui:
Como , a gente usa a série de Balmer. Que é a mesma coisa!
Agora a gente substitui o cm-1 e e calcula o
Passo 2
Bora lá:
Passo 3
Passo 4
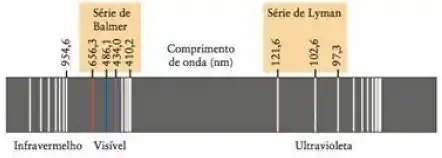
Pra identificar a linha do espectro a gente procura uma linha que esteja nesse comprimento de onda.
Aqui, o comprimento de onda calculado se refere à linha vermelha do espectro.
Resposta
.
Linha vermelha.