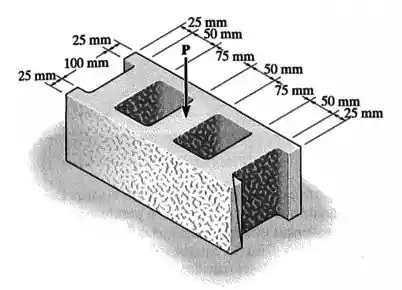
O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir , determine a maior carga vertical aplicada no centro que ele pode suportar.
Passo 1
Para que o material não falhe, é necessário que a tensão normal média seja menor que o seu valor máximo admissível :
Como e o esforço interno normal é igual a carga vertical externa :
O valor máximo de ocorre quando essa expressão é uma expressão de igualdade:
Precisamos calcular o valor da área da seção transversal do bloco para poder encontrar . Para tanto devemos observar a geometria da seção:
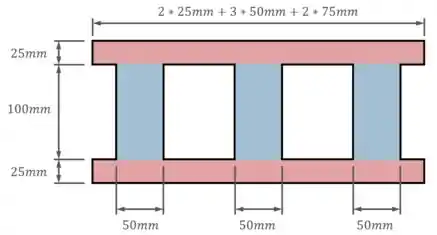
Passo 2
Primeiro, calculamos a área .
Na imagem acima vemos como a área da seção transversal do bloco pode ser dividida em áreas menores que se repetem.
Temos duas faixas longas iguais (pintadas de vermelho na imagem) e três “pontes” iguais (pintadas de azul).
Aproveitando essa simplificação, o cálculo da área fica assim:
Passo 3
Agora que temos a área, podemos voltar para a expressão que havíamos encontrado anteriormente:
Substituindo os valores de e :
Se lembrarmos que , podemos simplificar as unidades: