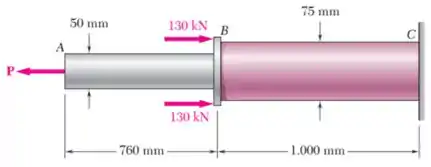
Duas barras cilíndricas de seção transversal cheia e são soldadas uma à outra em e submetidas a um carregamento conforme a figura. Determine a intensidade da força para a qual a tensão normal de tração na barra é duas vezes a intensidade da tensão de compressão da barra .
Passo 1
O exercício quer descobrir para que valor da força a relação a seguir é satisfeita:
Para calcular as tensões normais e , utilizaremos os seguintes dados:
- , uma vez que a barra está submetida somente à força de tração ;
- , uma vez que a barra está majoritariamente sobre compressão por parte das duas forças de , mas ainda está submetido também à força de tração ;
- , .
Como e estão em função de , as duas tensões, e , também vão ficar em função de .
Isso significa que quando usarmos a relação , vamos ter que manipular a expressão para isolar a força e descobrir o valor que ela deve ter.
Passo 2
A primeira coisa a fazer nesse exercício é calcular as tensões em e usando a fórmula da tensão normal média.
Para a barra , fica assim:
Já sabemos que .
Quanto à área , as barras possuem seção transversal circular, então podemos encontrar as áreas através da expressão . Como :
Não vamos simplificar mais essa expressão no momento pois essa tensão vai ser relacionada depois com a tensão , que também vai ter os termos “”, “” e “” na mesma posição.
Ou seja, vamos poder cortar esses termos com facilidade depois, como mostra a imagem abaixo:

Para a barra , como e :
Passo 3
Agora, aplicamos a relação :
Simplificando:
Isolando :
Calculando, isso dá: