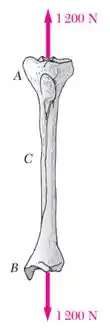
Um medidor de deformação localizado em na superfície do osso indica que a tensão normal média no osso é , quando o osso está submetido a duas forças de como mostra a figura.
Supondo que a seção transversal do osso em seja anular e sabendo que seu diâmetro externo é , determine o diâmetro interno da seção transversal do osso em .
Passo 1
As duas forças de geram esforços internos dentro do osso. Podemos fazer uma seção em e ver como, para garantir o equilíbrio, o esforço interno normal é igual a .
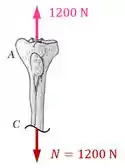
Esse esforço interno gera uma tensão normal média na seção transversal , que possui um formato de anel, como mostra a figura abaixo:
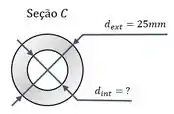
O exercício nos pede para descobrir o valor do diâmetro interno .
Precisamos primeiro encontrar qual é a área que a seção transversal deve ter, e, em seguida, relacionar essa área com .
Passo 2
Para que o esforço interno gere uma tensão , a seção transversal deve ter uma determinada área , como mostra a fórmula da tensão normal média:
Isolando a área :
Como :
Vamos guardar esse resultado!
Passo 3
A área da seção transversal é igual a área do círculo maior menos a área do círculo menor.
Mas lembra aí, a área do círculo é , onde é o raio do círculo. Como o raio é metade do diâmetro, podemos reescrever essa área do círculo como , ou, melhor ainda, !
Assim conseguimos calcular as áreas dos círculos maior e menor, e, consequentemente, calcular a área da seção, que é a diferença entre as áreas do círculo:
Queremos encontrar , então vamos isolá-lo!
Substituindo o valor fornecido de e o valor encontrado para a área :
Calculando tudo, isso dá: