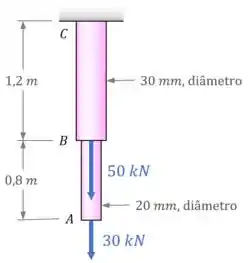
Duas barras circulares maciças são soldadas no ponto , como mostra a figura. Determine a tensão normal no ponto médio de cada barra.
Passo 1
Se a gente se lembrar da fórmula da tensão normal (), vamos ver como, para determinar as tensões normais médias de cada barra, precisamos saber:
- a força interna normal em cada barra;
- e a área da seção transversal de cada barra.
Então vamos pensar!
Quanto às forças internas: A barra está sobre ação somente da força de , então . Já a barra está sobre ação das forças de e , ou seja, .
E quanto às áreas das seções? Os diâmetros e podem ser usados para encontrar as áreas e .
Passo 2
Para a barra :
Para a área, vamos nos lembrar de que a área do círculo em função do seu diâmetro é :
Substituindo e :
Resultados assim em (também conhecido como ) não são muito comuns. Para resolver isso, podemos reescrever a força de como . Aí o resultado sai em (ou ):
Calculando tudo, isso dá:
Passo 3
Para a barra :
Mais uma vez, vamos escrever:
- a força interna em newtons (para que o nosso resultado saia em );
- a área do círculo em função do seu diâmetro ().
Com isso, a equação anterior fica assim:
Como :
Calculando tudo, isso dá: