Duas peças de madeira de seção retangular são coladas uma à outra em um entalhe inclinado, conforme mostra a figura. Calcular as tensões na cola para e para:
) ;
) ;
) .
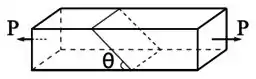
Passo 1
As peças estão sendo tracionadas por uma força e possuem uma seção transversal com área de dimensões .
O exercício quer que a gente avalie a tensão normal média e a tensão cisalhante média em uma seção angulada em relação à horizontal.
Para calcular essas tensões, vamos ter que:
- Fazer uma análise de esforços internos nessa seção inclinada para encontrar a força normal e a força cortante ;
- Observar a geometria da peça para encontrar a área da seção inclinada em função da área da seção transversal.
Feito isso, vamos ter que calcular os resultados para os diferentes valores de : , e .
Passo 2
Vamos começar pela análise de esforços internos na seção inclinada.
Para o equilíbrio das peças, a resultante das forças internas e no plano da cola deve ser igual à força :
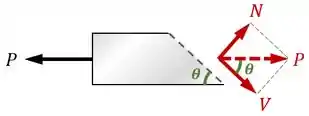
Observando essa imagem, tiramos que:
Passo 3
Agora, vamos encontrar a área da seção inclinada em função da área da seção transversal.
Observando a geometria da peça, vemos que :
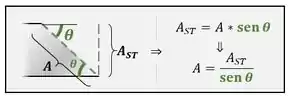
Passo 4
Agora que , e foram encontrados, podemos aplicar as fórmulas das tensões normal média e cisalhante média:
Substituindo os valores encontrados nos passos anteriores, temos:
Reorganizando essas expressões:
Se quiséssemos só o resultado literal, pararíamos aqui.
Para calcular os valores numéricos, vamos substituir e :
Fazendo a divisão e sabendo que , temos:
Como é um número pequeno, preferimos apresentar os resultados em .
Fazendo isso, obtemos que:
Agora, nos próximos três passos, vamos calcular os resultados para os três diferentes valores de .
Passo 5
Para o item ) , temos:
Sabendo que e , podemos calcular essas equações, obtendo os resultados:
Passo 6
Para o item ) , temos:
Aqui, uma coisa curiosa acontece.
Como , as duas tensões vão obter o mesmo resultado:
Se formos prestar atenção, esse resultado equivale a dividido por .
Passo 7
Finalmente, para o item ) , temos:
Sabendo que e , podemos calcular essas equações, obtendo os resultados:
E assim temos todos os resultados para responder a questão:
Resposta
) , ;
) ;
) , .