Calcule a eficiência com a qual a cunha, com inclinação de , eleva o peso , sob a ação da força horizontal atuando na cunha. O coeficiente de atrito entre a cunha e o bloco vale
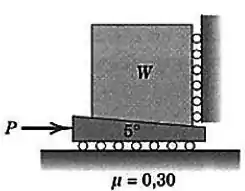
Passo 1
A eficiência será calculada por:
Qual será a força de entrada, que fornece o trabalho recebido? A força , que é a força que usamos como fonte de trabalho.
E qual é a força de saída, que gera o trabalho realizado? A força peso, já que vai ser ela que vai levantar o peso
Passo 2
Vamos analisar a cunha:
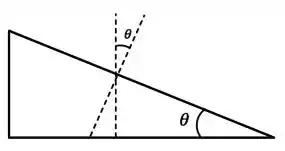
Entendeu a relação angular? Fizemos isso algumas vezes no capítulo anterior. Bem, o que falta? Falta a resistência que o peso exerce na cunha. Lembrando do ângulo de atrito fica assim:
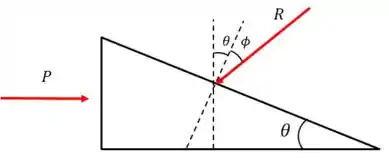
Precisamos achar as componentes horizontal e vertical da força :
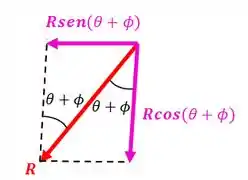
Pelo equilíbrio horizontal, teremos:
E pelo equilíbrio vertical temos:
Repare que a força de reação que a cunha exerce na caixa tem o mesmo módulo, mas sentido contrário à força representada.
Repare também que essa força tem uma componente vertical que equilibra o peso.
Passo 3
Agora, podemos escrever:
E:
Qual é a relação entre e? A mesma encontrada para e. Como a cunha é um triângulo retângulo:
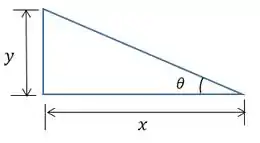
Assim, escreveremos:
Passo 4
Sendo assim:
Aqui temos que lembrar que o cálculo do ângulo de atrito é:
E é o ângulo da cunha que vale:
Então, a eficiência será: