De a um homem fica em pé sem se mover; de a ele caminha em linha reta com uma velocidade de . Quais são sua aceleração média no intervalo de a ? no intervalo de tempo de a ? Plote em função de, e indique como a resposta de podem ser obtidas a partir do gráfico.
Passo 1
Tanto no item quanto no o problema pede a aceleração média então vamos usar a mesma equação para resolver ambos
Passo 2
o intervalo dado é de a , por isso temos
Ainda pelo enunciado sabemos que a , pois o homem está parado, e a
Precisamos passar o tempo para segundos, assim achamos
Agora podemos aplicar a equação da
Passo 3
Vamos observar que o continua o mesmo
Passando para segundos temos:
E o também
O que implica que a é a mesma
Passo 4
Vamos fazer o gráfico de velocidade tempo :
Sabemos que ele não se move até e depois disso se move com , assim temos:
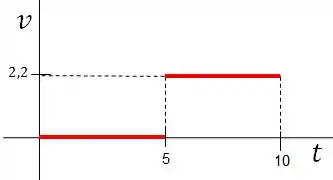
Vamos traçar uma reta entre os pontos estudados
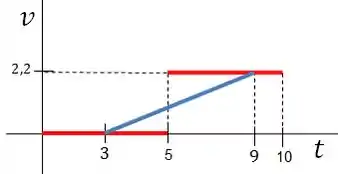
Agora Calculando a tangente da reta azul teremos a a
Já calculamos isso, e por isso quando transformarmos o tempo em segundo teremos
Resposta