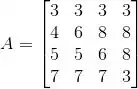Exercícios de Determinantes e Escalonamento - Lista de Exercícios Resolvida

Aplicamos em uma matriz as seguintes operações elementares:

trocamos com ;

multiplicamos por

Obtemos a matriz . Calcule .

Calcule:

Calcule, em função de , o determinante da matriz abaixo,

Diga qual das matrizes abaixo não tem determinante nulo:

Calcule o determinante da matriz abaixo:

(a)

(b)

(c)

(d)

Calcule o determinante da matriz

Calcule o determinante da matriz :

(a)

(b)

(c)

(d)

Seja uma matriz cujas colunas são os vetores e . Suponha que O determinante da matriz vale:

(a) 15

(b) 16

(c) 18

(d) 19

Seja

com reais arbitrários. Então:

Seja um inteiro. Assinale a alternativa correta:

se A e B são matrizes reais tais que , então ou

se é uma matriz real tal que , então existe uma matriz real não nula tal que

se e são matrizes reais e então existem infinitas matrizes reais tais que

se é uma matriz real tal que e é uma matriz real arbitrária, então

se e são matrizes tais que e , então

Sabendo que

Calcule, em função de :

Considere as matrizes e .

(a) Calcule o determinante de A. Esta matriz A é inversível?

Seja uma matriz cujas colunas são os vetores e Considere a matriz , cujas colunas são os vetores e Então:

(a)

(b)

(c)

(d)

Sejam e matrizes quadradas de ordem . Considere as seguintes afirmações:

Se através de uma operação que substitui uma linha por uma soma entre outras linhas, então .

, para todo .

Qual das opções abaixo é CORRETA?

A afirmativa é falsa e é falsa.

A afirmativa é verdadeira e é verdadeira.

A afirmativa é verdadeira e é falsa.

A afirmativa é falsa e é verdadeira.

Se

Então

É igual a

Calcule o determinante da matriz dada reduzindo à forma escalonada por linhas.

O determinante da matriz é:

Calcule .