Regra dos Trapézios
Produzido por Bruno PestanaTeoria
Introdução
Chega mais, tudo certinho? Vamos começar um assunto novo chamado Integração Numérica:
Veja bem, existem integrais que são muito difíceis e até mesmo impossíveis de resolver analiticamente, daquelas que só de olhar pensamos : “Cara, ta achando que eu sou uma calculadora?”.
Em outros casos, o valor de é conhecido só em alguns pontos da função e geralmente em um intervalo definido de [a,b]. Já que ninguém conhece a expressão analítica de não é possível calcular o valor da integral.
Tá, mas e daí? Aí é que entra a nossa digníssima Integração Numérica. Ela serve basicamente pra simplificar aquelas integrais monstruosas ou de funções desconhecidas. Tipo a de cima, cujo gráfico poderia ser:
Então, nós aproximamos a função de por um polinômio no intervalo [a,b] e achamos a integral do PRÓPRIO POLINÔMIO.
Bem mais fácil do que torrar os miolos resolvendo integrais de outros planetas né? Continua comigo, vamos no passo a passo que daqui a pouco você vai estar resolvendo integrais complexas de olhos fechados.
Regra dos Trapézios Simples
Agora nós chegamos em um ponto legal! Vamos começar a aproximar nossa função com um polinômio simples de primeiro grau de Lagrange com pontos igualmente espaçados entre si, com n=1 e de passo . Onde n é o número de iterações do método, ou seja, número de vezes que vamos aplicar o método, e h é o passo, ou seja, o espaço entre dois pontos consecutivos que usaremos.
Quando é igual a :
Então, acompanha comigo: Igualamos a integral a um polinômio interpolador, certo?
Esse polinômio simples é uma equaçãozinha da reta que une os dois pontos do intervalo até , dada por:
A integral do polinômio que interpola a função em e é:
Com o resultado da integral do polinômio chegamos na seguinte equação :
Agora, vamos pra um exemplo pra entender direitinho? Calcularemos a seguinte integral utilizando a regra dos trapézios simples:
Vamos dar uma olhadinha no gráfico da função no intervalo de 1 até 2? Consegue imaginar o que estamos fazendo?
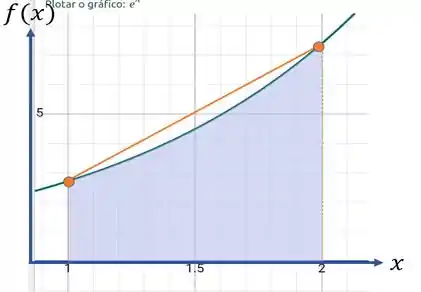
Pensa comigo, nós pegamos dois pontos da função e colocamos uma reta ligando os dois em a e b, conseguiu enxergar a fórmula geométrica do trapézio que aparece quando fazemos isso? Legal né!
Relembrando um pouquinho: Por definição Integral é a área sob a curva, e nós vamos nos concentrar na área do Trapézio pra solucionar a integral, lembra da fórmula para calcular a Área de um Trapézio?
Diz aí, fórmula da área do trapézio não é beeeeem parecida com a Integral? No nosso caso a altura () é a distância no intervalo [a,b] no eixo x em que a função está inserida e também o nosso passo já visto anteriormente, o trapézio menor é o e o trapézio maior é o .
Bem tranquilo né! Vamos tentar resolver, a primeira coisa que vamos calcular é o , sabendo que a função exponencial está em um intervalo de [1,2].
O próximo passo é substituir os valores na equação da Integral do polinômio:
No início do exemplo, eu mostrei que o valor real da Integral é 4,67077 e quando calculamos pela regra dos trapézios simples chegamos em um valor beeeeem diferente de 5,03668. Mas qual é o problema nisso tudo?
Esse método do trapézio simples vai funcionar quando tivermos um intervalo [a,b] relativamente pequeno, aí a aproximação da integral é aceitável. Se o intervalo tem uma amplitude muito maior, utilizar a aproximação com a área de um único trapézio não é indicada.
E como vamos quantificar o erro desse método? Ele pode ser determinado por:
Quando:
Sendo E um valor que obtemos de interpolações, podemos encontrar um limitante para o erro dessa forma:
Onde h é o passo e M2 é o valor máximo da segunda derivada da função:
Vamos voltar lá no gráfico e dar uma olhadinha na reta que liga os dois pontos e perceba que existe um espaço vazio (em verde) que não está sendo considerado, entendemos o erro com a área entre o trapézio e a .
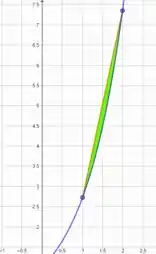
Regra dos Trapézios Repetida
Aí nós chegamos na regra dos Trapézios Repetida que é mais adequada quando temos um intervalo [a,b] de grande amplitude. Então nós somamos a área de n trapézios, cada um definido em seu subintervalo, aplicamos a regra do trapézio para descobrir a área em caaaaaada intervalo, sacou?
Vamos analisar o gráfico daquela mesma função que calculamos pela regra dos trapézios simples, só que agora vamos analisar a área de cada um dos subintervalos. Perceba que agora temos uma curva com n trapézios dentro dela.

Isso significa que a integral, ou seja, a área sob a curva é dada pela soma das integrais definidas em cada intervalinho com amplitude , que será tanto a altura dos trapézios quanto o passo. Logo, nosso passa a ser:
Ou seja, os pontos estão igualmente espaçados entre si.
Brincando com as integrais, chegamos na seguinte equação:
Fica a dica para lembrar da fórmula: se pegarmos a área de dois trapézios desse tipo:
Se pegarmos 3 deles:
Então, repare que todos os valores da função, menos o primeiro e o último, ficam multiplicados por 2. 😉
Voltando.
Se é o tamanho dos subintervalos, nosso erro vai ser limitado por:
Onde n é o número de vezes que utilizamos a regra do trapézio.
Vamos resolver o exemplo utilizando agora a regra dos trapézios repetido agora que você já está mandando bem, definiremos o valor de n =4.
Vamos retomar, a idéia é mesma que usamos na regra dos trapézios simples. Lembra qual foi a primeira coisa que calculamos? Show! Vamos calcular o para determinar a amplitude dos intervalos:
É muito comum em cálculo numérico utilizarmos de métodos iterativos, ou seja, que dependem do passo anterior. E nesse caso não é diferente. Vamos pensar que temos iterações (k) que vão de 0 até n. O valor de k=0 é sempre referente ao e k=n sempre referente ao .
Beleza, mas o que isso significa?
Significa que os outros subintervalos então dentro de 0 até n, mas precisam ser calculados. E é aí que entra o , ele determina a distância entre um intervalo e outro sempre com base no passo anterior .
Vamos montar uma tabelinha que aí você já vai entender o que eu estou querendo dizer:
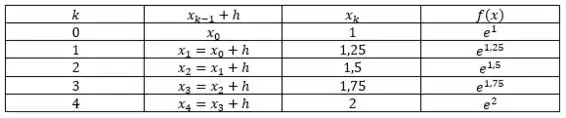
Observe na tabela que temos as iterações k, e a cada iteração acrescentamos para descobrir o que será aplicado na função.
Então, é só substituir na fórmula:
O resultado já está se aproximando do valor real né, que é 4,67077? Show de bola! Isso significa que quando mais subintervalos n eu colocar mais próximo o valor fica do real. Com isso, vamos calcular o erro:
Calculando :
Dessa forma:
A teoria fica por aqui, #PartiuExercícios ?
Regra dos Trapézios Repetida
Exercícios Resolvidos
Exercício Resolvido #1
Lista 5 – Professor Mauro – UFRJ – Questão 4
Dê um exemplo de uma função onde a regra dos trapézios calcula o valor exato da integral.
Passo 1
Bom, essa regra aproxima nossa função por uma reta, certo? Então ela vai calcular o valor exato para a integral de qualquer polinômio de grau ! Porque nesses casos, não teremos erro em nossa aproximação.
Resposta
Qualquer polinômio de grau .
Exercício Resolvido #2
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 312, exercício 5
Qual o erro máximo cometido na aproximação de pela regra dos Trapézios com quatro subintervalos?
Passo 1
Nesse exercício trabalharemos com a função :
Vamos relembrar a fórmula do erro:
Onde é a quantidade de subintervalos e é o passo, ou seja, a diferença entre dois pontos consecutivos do intervalo.
Além disso, temos que o intervalo de é:
e .
Passo 2
Bom, como o enunciado pede para fazermos subintervalos, e, para achar o passo , temos que dividir o intervalo de a em quatro partes iguais, ou seja:
Agora que descobrimos o passo, vamos calcular agora a segunda derivada da função:
Vamos calcular o valor máximo de no intervalo .
Como é uma função linear crescente, quanto maior o maior . Logo o máximo fica em e vale . Substituindo todas essas informações na fórmula:
Um erro bem grande né!
Resposta
Exercício Resolvido #3
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 301, exemplo 1
Seja
Calcule uma aproximação para usando subintervalos e a regra dos Trapézios repetida. Estime o erro cometido.
Qual o número mínimo de subdivisões de modo que o erro seja inferior a ?
Passo 1
Primeiro vamos montar uma tabelinha dessa função! Como ele quer uma divisão em subintervalos teremos . Ficamos então com o seguinte:

Já até botei a soma no final porque sei que vamos precisar haha.
Aplicando a fórmula:
Como temos a tabelinha acima com a soma no final, olha só a malandragem que faremos! Adicionaremos e depois subtrairemos e na nossa aproximação:
Passo 2
E agora podemos encontrar um limitante para o erro que é dado por:
Como o máximo de no intervalo acontece em e tem como valor , o erro fica:
Passo 3
Queremos que o erro seja menor que . Pegando aquela mesma fórmula do erro, temos:
Tomando só os valores positivos de :
Logo, o menor valor de para termos esse limitante de erro é .
Resposta
Exercício Resolvido #4
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 311, exercício 1
Calcule as integrais a seguir pela regra dos Trapézios usando quatro e seis divisões de .
Passo 1
A primeira integral é:
Para 4 divisões:
Temos que
Sabemos que a regra dos trapézios reduzida é dada por:
Percebeu que todo mundo ali foi multiplicado por 2, menos o primeiro e último termo? Bom, isso quer dizer que se multiplicar a soma dos elementos por 2, vamos ter:
E se subtrairmos o primeiro e o último termo dessa equação:
Ou seja:
Isso facilita a nossa vida, porque ao invés de ficar multiplicando um monte de valores por 2, basta multiplicar a soma dos números e , dessa soam, subtrair o primeiro e último termo.
Montamos a nossa tabelinha:

E aplicamos a fórmula:
Só isso! Nada demais né?
Passo 2
E para 6 divisões:
Agora . Novamente montamos nossa tabelinha:

E aplicamos a fórmula:
Passo 3
Próxima integral!
Com 4 divisões:
Temos que . Jogando na tabela:

Agora na fórmula:
Passo 4
Para 6 divisões:
Agora . É só passar pra tabela:

E mandar bala na fórmula:
Passo 5
Eu sei, de novo?! Sim, mas é a última integral, seja forte! Haha
Para 4 divisões:
. Na tabela:

Na fórmula:
Passo 6
Último passo! Agora para 6 divisões:
Temos . Jogando na tabela:

E na fórmula:
Resposta
4 divisões:
6 divisões:
4 divisões:
6 divisões:
4 divisões:
6 divisões:
Exercício Resolvido #5
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 312, exercício 2
Usando as integrais do exercício anterior com quantas divisões do intervalo, no mínimo, podemos esperar obter erros menores que ?
Passo 1
As integrais do último exercício foram:
E a fórmula do limitante do erro que vamos usar para elas é:
Com um limitante de e sabendo que , temos:
Passo 2
Temos:
O máximo de no intervalo é . E . Na fórmula:
Logo, o menor para obtermos o erro desejado é .
Imagina fazer isso tudo na mão!

Passo 3
Temos:
Como ela é sempre crescente e negativa, o módulo máximo de no intervalo acontece em , onde . E nesse caso . Substituindo:
Então, o menor para um erro de é .
Passo 4
Por último temos:
O máximo do módulo da derivada segunda no intervalo ocorre em , onde . E temos . Na fórmula:
Então agora o menor seria !

Que bom que computadores existem!
Resposta
.
.
.
Exercício Resolvido #6
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 312, exercício 3
Calcule o valor aproximado de com três casas decimais de precisão usando a Regra dos Trapézios.
Passo 1
Pra começo de conversa se o cara quer três casas decimais de precisão então queremos um erro menor ou igual a ! Com isso conseguimos achar o número de divisões pela fórmula:
Temos que e sabemos que o limitante do erro é . Além disso, temos que:
Sendo assim, o valor máximo de no intervalo fica em e vale . Substituindo todas essas informações na fórmula:
Logo, o menor valor de (que obviamente é o que vamos usar pra termos menos trabalho) que garante uma precisão de é .
Passo 2
Como , temos que . Montando nossa tabela:

Jogando na fórmula:
Resposta
Exercício Resolvido #7
Lista de Exercícios - FEI
Determinar o menor número de pontos necessários para calcular a integral pela regra do trapézio com erro inferior a 0,001
Passo 1
Fala galera, bom nesses casos onde o professor pergunta pra gente qual o número de pontos necessário, a gente vai se apegar com força na fórmula do limitante de erro, que é essa aqui oh:
Com ela a gente vai conseguir calcular o passo que é o “h” e já já te mosto como o h leva a gente até o número de pontos.
Essa parte mais a direita da fórmula meio estranha só quer dizer que eu preciso achar o máximo valor do módulo da derivada segunda no intervalo onde eu estou integrando..então bora derivar! Essa é mole...
No nosso intervalo de integração, o valor de x que faz ser máximo é x=0 . Nesse caso a fórmula do erro ficaria:
Se o erro é sempre menor ou igual a e queremos limitar ele à 0.001, Então podemos escrever:
Passo 2
Bom ta na hora de usar aquela sacada que o professor acha que vc não manja. Podemos escrever h desse jeito aqui:
O b e o a são os extremos superior e inferior da integral e n o número de intervalos. E veja só
O número de pontos necessários k é o número de intervalos mais um, viu só como o h salvou nossa vida!!! Nesse exercício o intervalo de integração é então...
Passo 3
Substituindo na nossa inequação:
Resolvendo ficamos com...
Invertendo de ambos os lados
Isolando ficamos com
Elevando a meio ambos os lados
Passo 4
Com deve ser um número inteiro, sempre vamos arredondá-lo para cima, nesse caso .
Como a pergunta foi o número de pontos e não de intervalos (pegadinha do professor), é só somar 1 ao número de intervalos .
Resposta
pontos
Exercício Resolvido #8
Elaboração própria
Seja uma função linear que se deseja integrar no intervalo [d,e] através do método do trapézio. Justifique matemáticamente porquê este método é tão bom quanto qualquer outro com relação ao erro para este caso.
Passo 1
Logo de cara esse enunciado trás a primeira dica né, é uma função linear, logo podemos imaginar
E a fórmula do limitante de erro é essa aqui:
Olhando pra fórmula dá pra gente sacar que ela depende da derivada segunda da nesse caso, para uma função linear, a derivada seria zero, e portanto o erro também.
Resposta
Não se comete erro ao integrar a