Exercícios de Método de Gauss-Seidel - Lista de Exercícios Resolvida

Em cada caso verifique se o critério de Sassenfeld é satisfeito e resolva por Gauss-Seidel com , se possível:

Dar exemplo de um sistema de equações que não seja diagonal dominante, mas seja convergente usando o método de Gauss-Seidel.

Obs.: Um sistema é diagonal dominante se para todas as linhas da matriz de coeficientes, o módulo do valor da matriz na diagonal é maior que a soma dos módulos de todos os demais valores (não-diagonais) daquela linha. 

Dado o sistema linear abaixo. Use precisão

1. O que é possível dizer sobre a sua convergência quando utilizado o método de Gauss- Seidel?
2. Permutando-se as equações, seria possível garantir convergência para um chute inicial ?

Se possível, resolva o sistema para o chute inicial. Use

Considere o seguinte sistema de equações lineares:

Mostre que este sistema não satisfaz o critério de linhas;

Mostre que esse sistema não satisfaz o critério de Sassenfeld;

O que se pode afirmar sobre a convergência dos métodos de Gauss-Jacobi e Gauss-Seidel, quando aplicados a este sistema?

Mostre que o sistema obtido permutando-se as duas primeiras equações satisfaz o critério de Sassenfeld;

Usando o método de Gauss-Seidel, determine a solução aproximada do sistema, com a permutação sugerida no item anterior e erro .

Considere o sistema linear:

Escreva um sistema linear equivalente tal que o método de Gauss-Seidel convirja.

Aplique o método de Gauss-Seidel para resolver o sistema modificado utilizando e com precisão de .

Resolva o sistema linear:

Pelo método de Gauss-Seidel com e

Resolva pelo método iterativo de Gauss-Seidel, se possível. Use precisão

Seja o sistema linear:

É possível dizer que o Método de Jacobi é convergente para este sistema?

E o de Gauss-Seidel?

Resolva o sistema utilizando o método de Gauss-Seidel com , tolerância de .

3. Complete o programa abaixo para implementar o método de resolução de sistemas lineares de Gauss-Seidel. Considere que as funções carregarSistemaLinear, diferencaMaxima e imprimirX já estejam implementadas.

1. Dado o sistema linear:

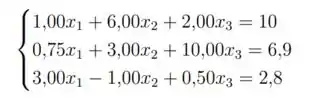
1. Reescreva o sistema linear de forma a garantir sua convergência pelo método de Jacobi (diagonal estritamente dominante por linha).
2. Escreva as expressões das sequências obtidas pelos métodos de Jacobi e Gauss-Seidel (i.e., o motor gerador de cada incógnita) para o problema acima.
3. Calcule duas iterações do método de Gauss-Seidel com vetor inicial x(0) = (0; 0; 0)T .

4) e são vetores do . Queremos determinar qual é o vetor do espaço gerado por e que se encontra mais próximo ao vetor , na norma Euclidiana, o que nos leva a um problema de mínimos quadrados. Sabemos que os produtos escalares entre os vetores são:

, , , , ,

E que as normas ao quadrado de e são iguais a 8.

a) Ordene os vetores da base de forma conveniente para garantir que o método de Gauss-Seidel quando aplicado ao sistema resultante seja convergente.

4) e são vetores do . Queremos determinar qual é o vetor do espaço gerado por e que se encontra mais próximo ao vetor , na norma Euclidiana, o que nos leva a um problema de mínimos quadrados. Sabemos que os produtos escalares entre os vetores são:

, , , , ,

E que as normas ao quadrado de e são iguais a 8.

b) Calcule 1 iteração de Gauss-Seidel a partir da aproximação inicial nula e delimite o erro (em relação à solução exata do sistema linear) após esta iteração.

4) e são vetores do . Queremos determinar qual é o vetor do espaço gerado por e que se encontra mais próximo ao vetor , na norma Euclidiana, o que nos leva a um problema de mínimos quadrados. Sabemos que os produtos escalares entre os vetores são:

, , , , ,

E que as normas ao quadrado de e são iguais a 8.

c) Estime o número de iterações para garantir um erro menor que

Erro para o método de Gauss-Seidel:

Valores de Logaritmos: ,