Método De Gauus-Seidel
Teoria
Fala aí! Hoje vamos aprender um pouquinho melhor sobre o método de Gauss-Seidel, que é um método iterativo para a resolução de sistemas lineares!
Tá preparado? Então vem comigo descobrir o tanto que esse método é parecido com o de método de Jacobi. E se você só quiser o algoritmo desse negócio relaxa que separei pra você lá no final. 😆
⭐ Veja também ⭐
- Lista de Exercícios Resolvidos de Método de Gauss-Seidel.
- Método da Eliminação de Gauss para a resolução de Sistemas Lineares.
- Método de Gauss-Jacobi.
- Quer aprender a programar?
Para que serve o Método de Gauss-Seidel?
O método de Gauss-Seidel fornece uma receita para resolver sistemas lineares mais complicados.
Ele é uma adaptação do método de Jacobi com a intenção de acelerar a convergência. Quer dizer que vamos chegar na resposta desejada com um número menor de iterações, isto é, precisaremos repetir o processo descrito pelo método um número menor de vezes.
E como funciona esse negócio aí?
Te explico agora! Para se calcular a componente
Ficou confuso com esse tanto de letra que apareceu aí? Calma, vou desenhar pra deixar tudo bem claro pra você!
Se liga nesse sisteminha aqui:
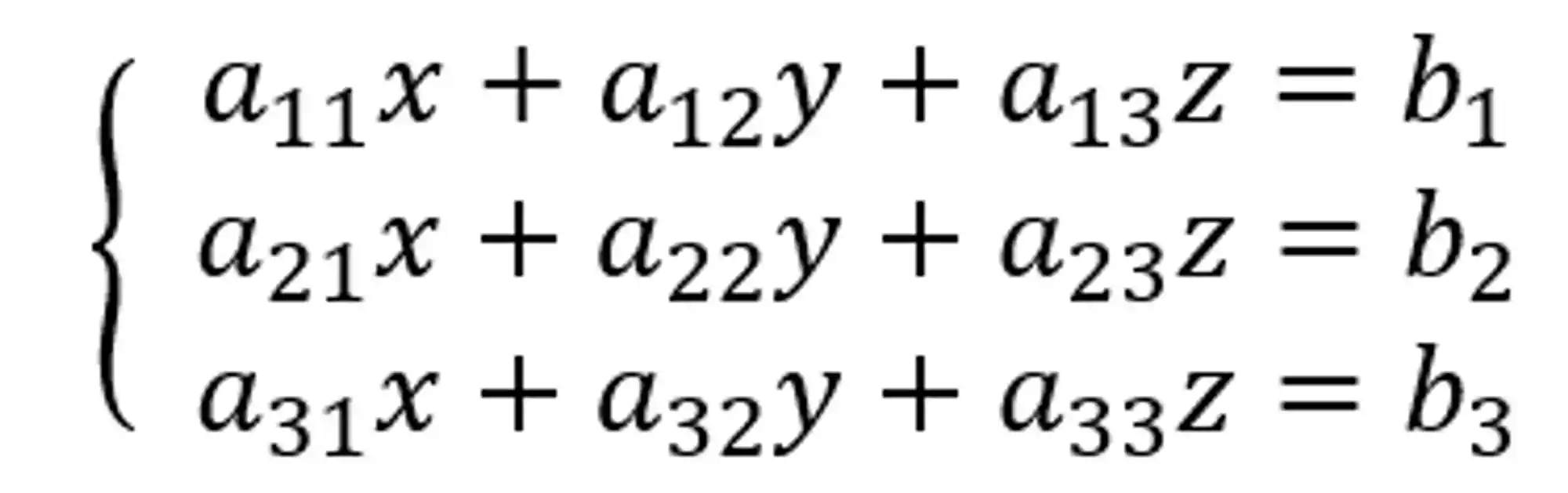
Só pra deixar claro:
O método de Gauss-Seidel diz que encontramos a função de iteração para a variável
Esse índice
Aí, vamos repetir isso aí para as outras linhas do sistema, para obtermos as funções de iteração das outras variáveis.
Da segunda equação, vamos isolar o
Opa! Por que o índice do
Aaah, chegamos na grande sacada do método de Gauss-Seidel!
Como a gente já tem um valor atualizado pra variável
Já consegue me dizer como vai ficar a função de iteração da variável
Da terceira equação, vamos isolar o
Muito bem!! Naquele mesmo esquema: já temos um valor atualizado pra variável
Saca só nesse esqueminha aqui de como vai ficar cada iteração pelo método de Gauss-Seidel:
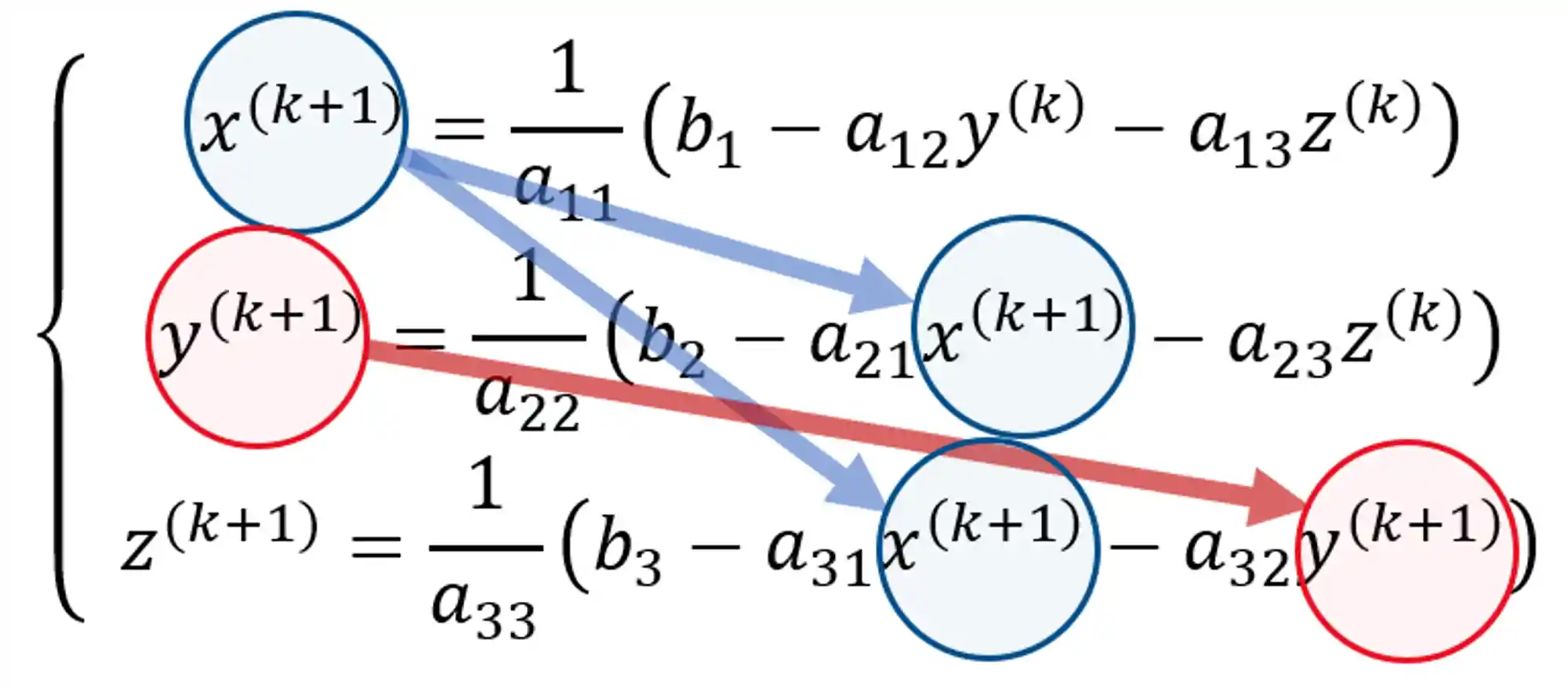
Já vamos fazer um exemplo pra deixar isso bem fixado na sua cabeça. Mas tem algumas coisinhas que precisamos ver antes disso!
Se quiser, pode assistir esse vídeo aqui explicando tudo isso bonitinho também 👇
Critério de Convergência (Critério de Sassenfeld)
Antes de começarmos a usar esse método de Gauss-Seidel, precisamos ter certeza que o sistema vai convergir.
O critério de Sassenfeld é condição suficiente para a convergência do método, e ele diz o seguinte:
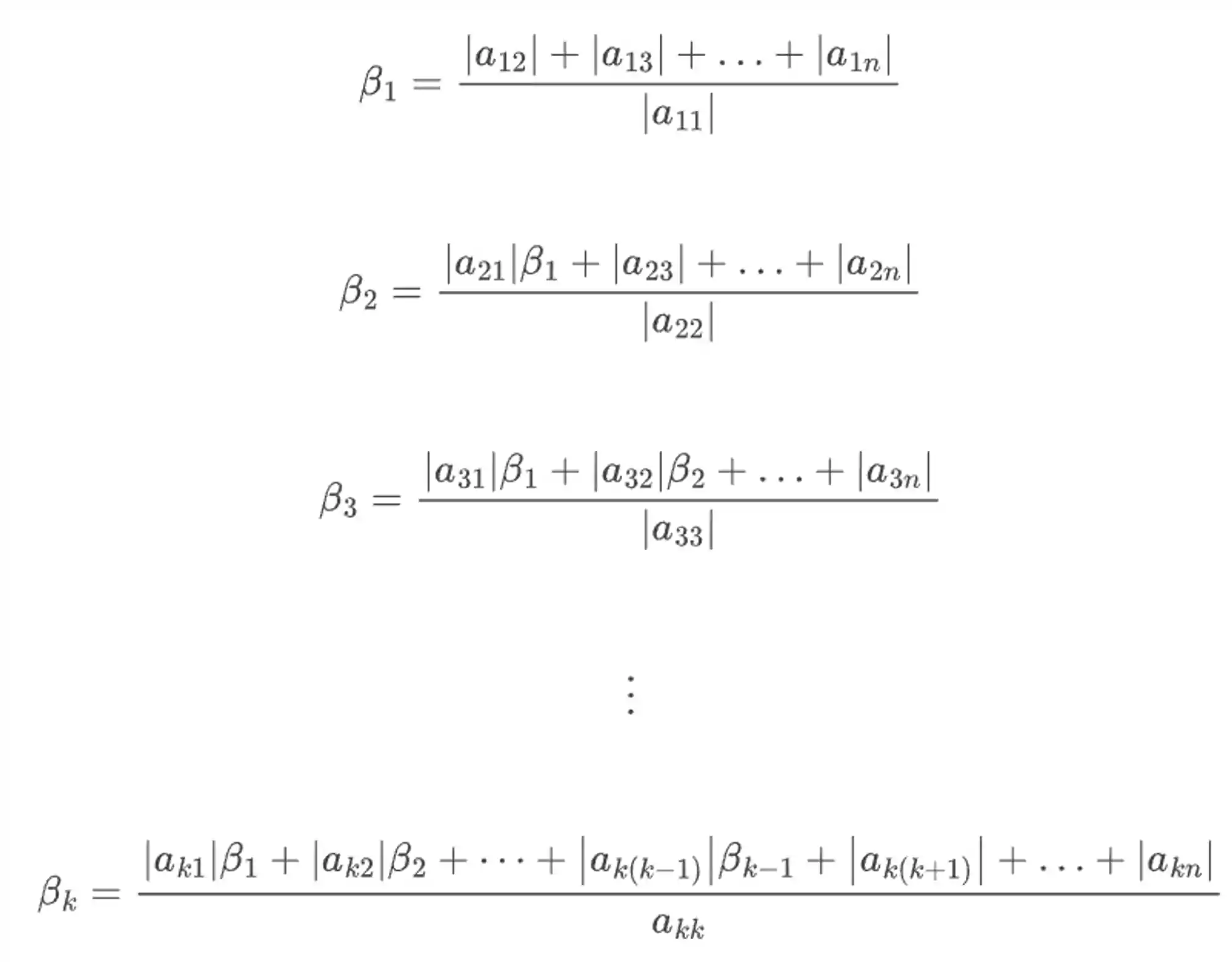
Depois de calcular todos os
Critério de Parada
Beleza, já sabemos como funciona o método e quando podemos utilizá-lo. Mas, depois que começar as iterações, tem algum jeito de perceber que já encontramos uma aproximação boa o suficiente?
Claro que tem!
O critério de parada normalmente utilizado são as diferenças
Quando a maior dessas diferenças, em módulo, for menor que o erro informado pelo enunciado, quer dizer que já temos uma aproximação boa o suficiente e podemos parar com as iterações.
Tranquilo? Agora sim, temos tudo o que precisamos pra resolver um exercício.
Exemplo: Resolva o sistema linear abaixo pelo método de Gauss-Seidel com
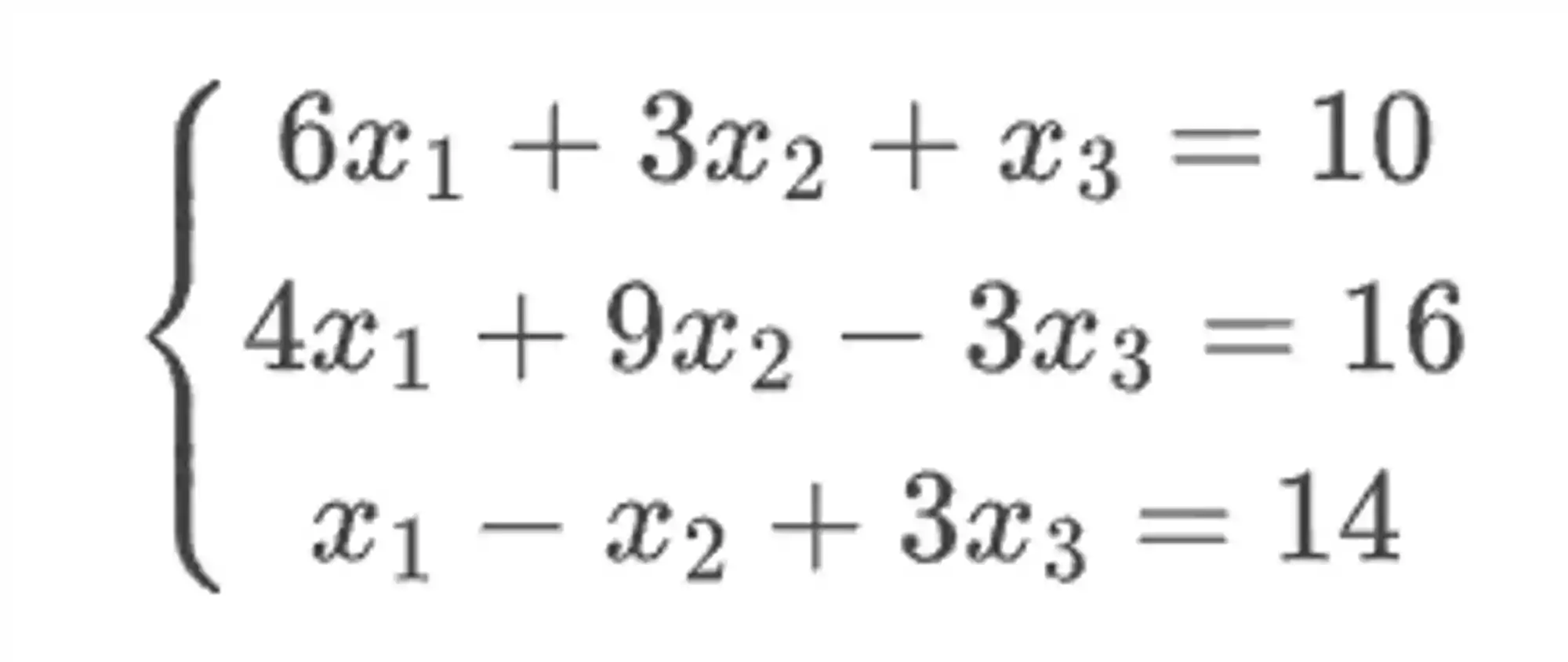
Passo 1: Aplicar o critério de convergência.
Antes de começar, temos que ver se esse negócio aí vai convergir, né? Se não, só vamos perder nosso tempo fazendo conta à toa.
Pelo critério de Sassenfeld:
O máximo aí é o
Passo 2: Encontrar as funções de iteração.
Só isolar a primeira variável na primeira equação, a segunda variável na segunda equação e assim por diante.
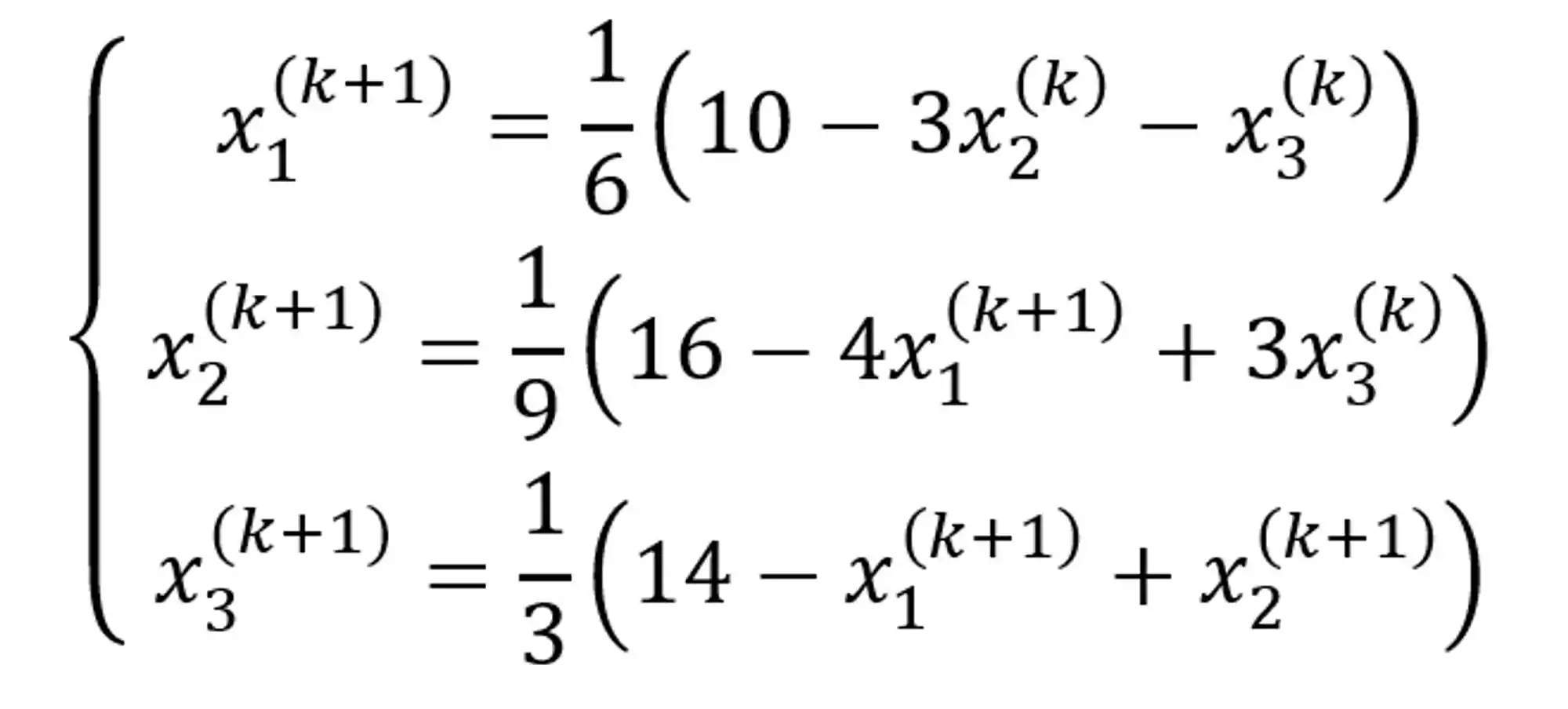
Tranquilo, né? Isso aí já mostrei como que faz ali em cima.
Ah, um detalhe: toma muito cuidado com os sinais. Se você reparar ali na segunda equação ficamos com
Passo 3: Primeira iteração.
Começamos lá pelo
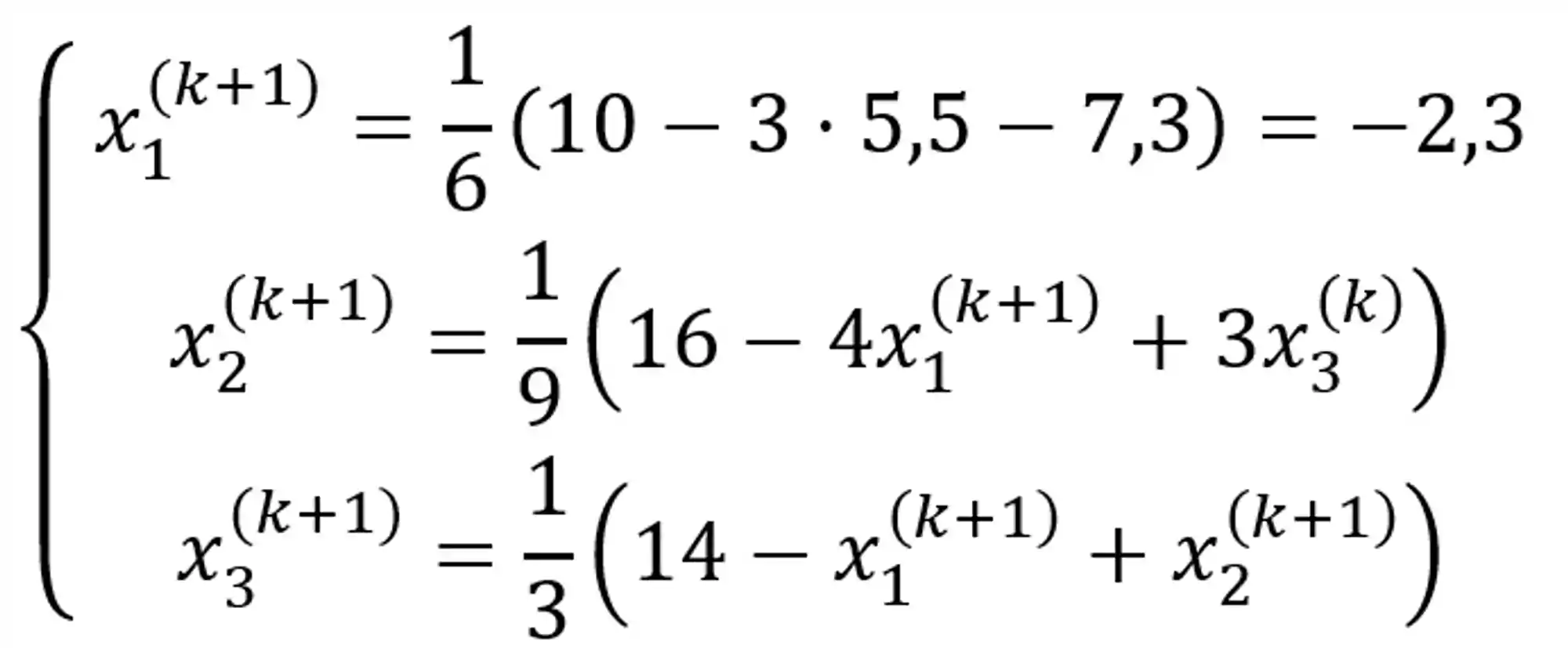
Esse valor encontrado para o
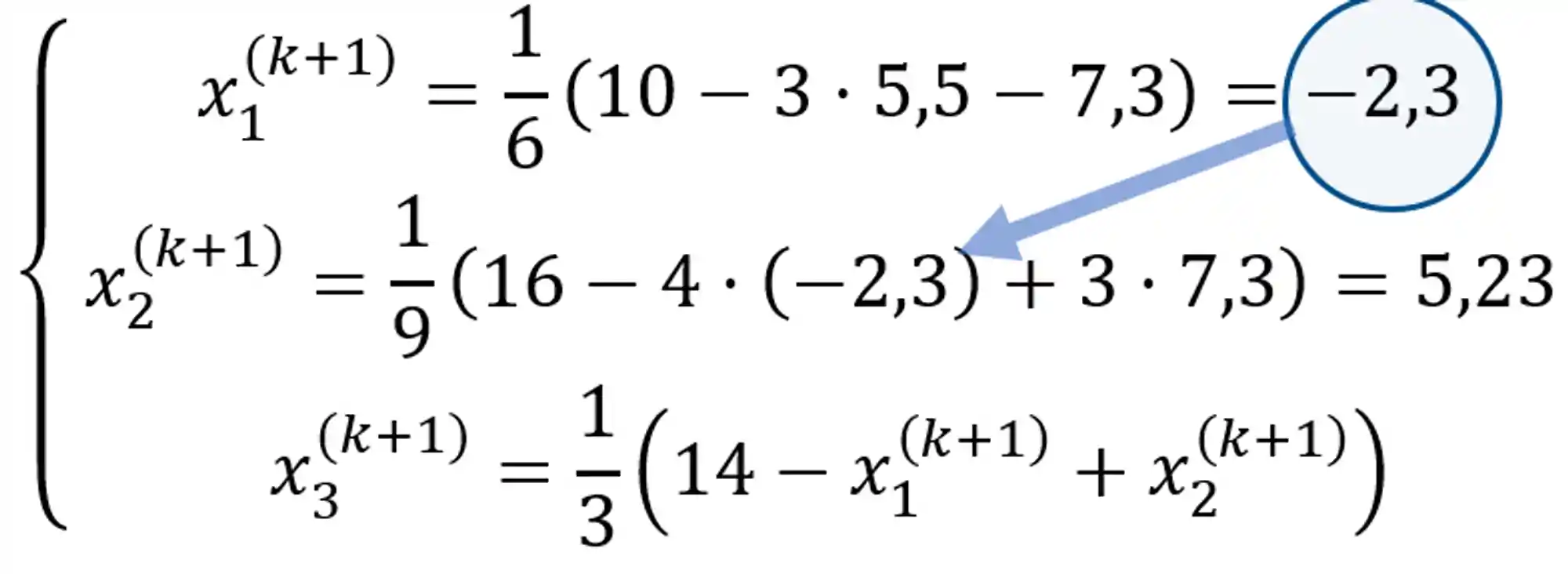
E para a última equação:
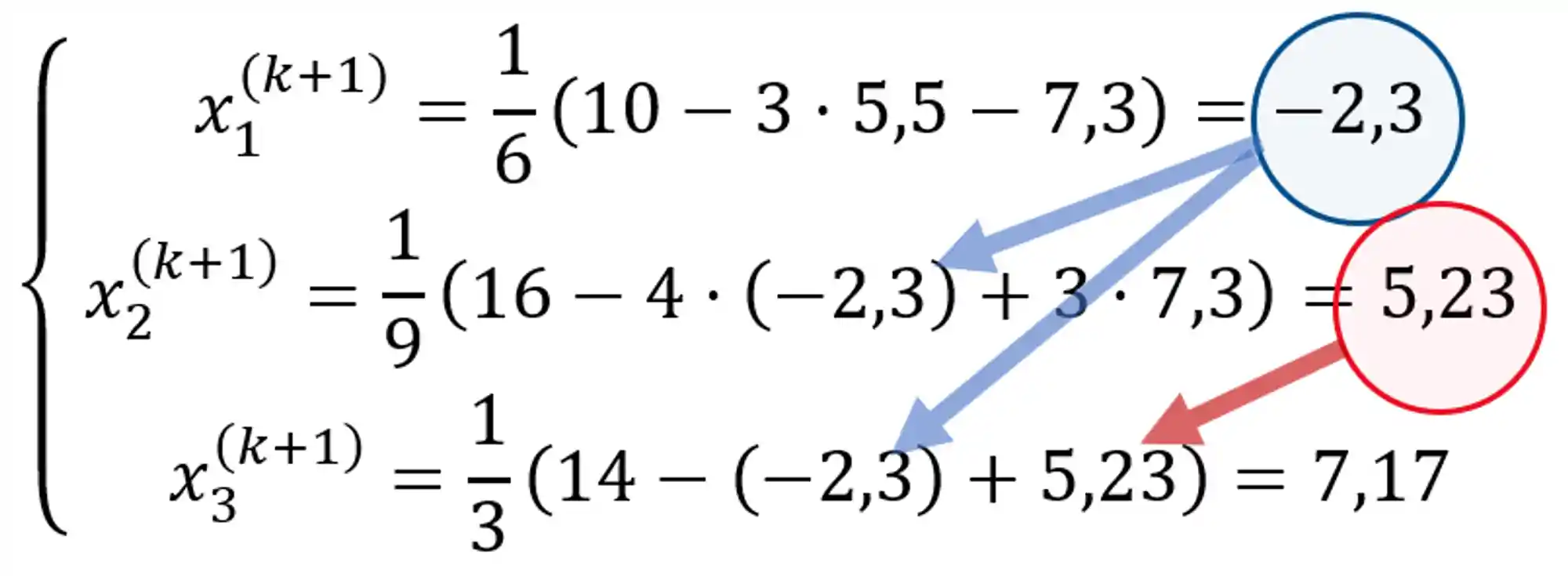
Beleza, ficamos com
Passo 4: Analisar o critério de parada.
A maior diferença aqui vai ser para o
Nossos valores ainda não são bons o suficiente. Devemos fazer mais iterações, cada vez com os valores atualizados para nossas variáveis!
Algoritmo do Método de Gauss-Seidel
A grande vantagem do Cálculo Numérico é que podemos escrever algoritmos e soltar tudo isso no cérebro dos nossos computadores pra eles se virarem, não é? Então bora ver como fica o algoritmo desse método aqui!
Agora você já tem todas as informações necessárias pra resolver nossa lista de exercícios 😉
Exemplo: Resolva o sistema linear abaixo pelo método de Gauss-Seidel com e .
Algoritmo do Método de Gauss-Seidel
Exercícios Resolvidos
Exercício Resolvido #1
Lista 3 – Professora Angela – UFRJ – Questão 11
Dar exemplo de um sistema de equações que não seja diagonal dominante, mas seja convergente usando o método de Gauss-Seidel.
Obs.: Um sistema é diagonal dominante se para todas as linhas da matriz de coeficientes, o módulo do valor da matriz na diagonal é maior que a soma dos módulos de todos os demais valores (não-diagonais) daquela linha.
Passo 1
Beleza, o enunciado dá uma breve explicação do que é um sistema diagonal dominante. Em um sistema isso significa:
E para que o sistema convirja pelo método de Gauss-Seidel temos que satisfazer o critério de Sassenfeld, que em um sistema fica:
E queremos que e . Para que isso seja satisfeito sem usarmos um sistema diagonal dominante, basta que e que por exemplo. Se liga:
No sistema acima temos:
Logo, o sistema converge pelo método de Gauss-Seidel, mas o sistema não é diagonal dominante.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 185, exercício 22.
Em cada caso verifique se o critério de Sassenfeld é satisfeito e resolva por Gauss-Seidel com , se possível:
Passo 1
Verificando o critério de Sassenfeld:
Logo, . O critério é satisfeito.
Passo 2
As funções de iteração são:
Visualmente podemos ver que a solução é simplesmente né? Mas pra treinar um pouco vamos usar como aproximação inicial .
Iteração :
Então temos .
Critério de Parada:
Não atingimos o critério, então continuamos as iterações.
Iteração :
Então temos .
Critério de Parada:
Não atingimos o critério, então continuamos as iterações.
Iteração :
Então temos .
Critério de Parada:
Não atingimos o critério, então continuamos as iterações.
Iteração :
Então temos .
Critério de Parada:
Beleza, o critério de parada foi atingido! Então nossa aproximação é:
Passo 3
Aplicando o critério de Sassenfeld temos:
Logo, . O critério é satisfeito.
Passo 4
As funções de iteração são:
Agora precisamos de um chute inicial. Se a gente jogar em todas as variáveis dá valores bem próximos né? Então vamos usar .
Iteração :
Então temos .
Critério de Parada:
Não atingimos o critério, então continuamos as iterações.
Iteração :
Então temos .
Critério de Parada:
Não atingimos o critério, então continuamos as iterações.
Iteração :
Então temos .
Critério de Parada:
Não atingimos o critério, então continuamos as iterações.
Iteração :
Então temos .
Critério de Parada:
Não atingimos o critério, então continuamos as iterações.
Iteração :
Então temos .
Critério de Parada:
Não atingimos o critério, então continuamos as iterações.
Iteração :
Então temos .
Critério de Parada:
Beleza, o critério de parada foi atingido! Então nossa aproximação é:
Resposta
Exercício Resolvido #3
Lista 3 – Professor Mauro – UFRJ – Questão 1
Considere o seguinte sistema de equações lineares:
Mostre que este sistema não satisfaz o critério de linhas;
Mostre que esse sistema não satisfaz o critério de Sassenfeld;
O que se pode afirmar sobre a convergência dos métodos de Gauss-Jacobi e Gauss-Seidel, quando aplicados a este sistema?
Mostre que o sistema obtido permutando-se as duas primeiras equações satisfaz o critério de Sassenfeld;
Usando o método de Gauss-Seidel, determine a solução aproximada do sistema, com a permutação sugerida no item anterior e erro .
Passo 1
Verificando o critério das linhas:
Só pelo já podemos ver que ele não satisfaz o critério.
Passo 2
Verificando o critério de Sassenfeld:
Novamente, apenas pelo valor de já sabemos que o critério não é satisfeito.