Área de Curvas Parametrizadas
Produzido por Mariana PessanhaTeoria
Revisão de Conceitos
E aí gente, tudo bem? Você provavelmente já deve ter estudado área entre curvas e eixos e área entre curvas. Então, o que há de novo?
A diferença é que antes as curvas não estavam parametrizadas, ou seja, elas estavam expressas em suas equações cartesianas: ou . Agora, vamos ter algo do tipo e .
Tínhamos basicamente 3 casos:
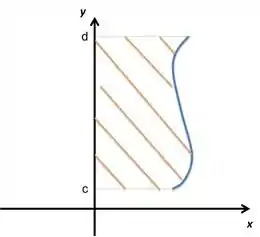
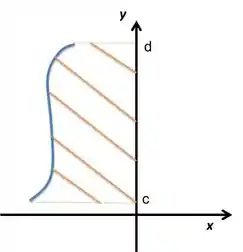
- Áreas entre a curva e o eixo , assim como na figura a seguir:
- Área entre a curva e o eixo , como no exemplo:
- Área entre curvas, como a seguir:
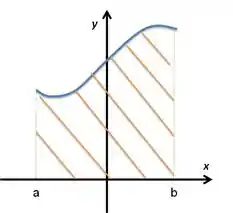
Sua área é dada por:
Ou ainda
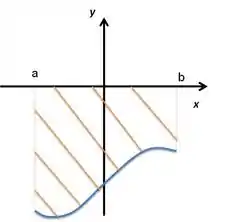
Onde a área é:
Com área:
Ou ainda
Onde a área é:
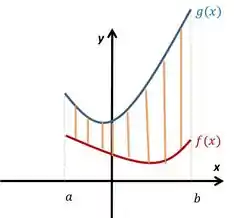
Com área:
Vamos ver que com curvas parametrizadas, usaremos o mesmo raciocínio.
Calculando área de curvas parametrizadas
Quando tivermos uma curva parametrizada, basicamente o que vamos fazer é identificar em qual das situações do cálculo de áreas acima apresentados o problema se encaixa.
Vamos utilizar a fórmula adequada conforme estudado, porém temos que tomar cuidado com alguns detalhes, como substituir o ou por e , respectivamente, substituir ou em função de e rever os limites de integração.
Calma que vamos ver isso tudo que eu falei no exemplo a seguir e também nos exercícios resolvidos.
Vamos ver um exemplo:
Exemplo :
Determine a área da ciclóide
Passo 1: Verificar se há trechos repetidos
Repare também que não há trechos repetidos da curva, ou seja, a curva não percorre um mesmo caminho duas vezes, pois parar todo , com . O esboço da cicloide se encontra na abaixo:
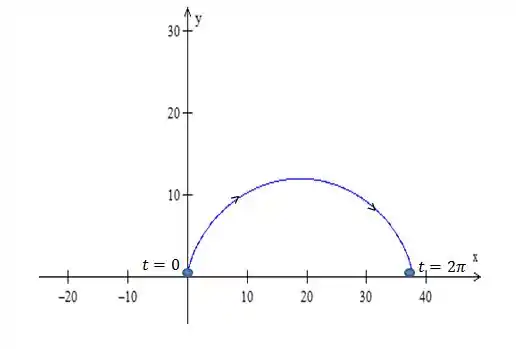
Passo 2: Identificar qual dos 3 tipos de cálculo de áreas vamos usar
Primeiramente, podemos perceber que é sempre não negativo, pois . Sabemos então que se trata do caso em que temos de calcular a área entre a curva e o eixo .
Passo 3: Expressar a integral e os limites de integração em relação a .
A fórmula para calcular sua área é:
Primeiramente, vamos começar identificando :
Agora, vamos encontrar :
Logo temos
Falta definir os limites de integração! Ele é dado pelo valor de no início da curva e no fim da mesma. Logo, e
A fórmula para calcular a área fica então:
Substituindo:
Passo 4: Calcular a integral
Partiu exercícios?!