Limite Trigonométrico Fundamental
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí, você acaba de chegar no Responde Aí! Então bora lá aprender sobre Limite Fundamental Trigonométrico?
Limite Fundamental Trigonométrico
Existem alguns limites que são mais complexos de resolver, temos que utilizar ferramentas um pouco mais avançadas para achar a solução, mas que são bem comuns, ou seja, aparecem toda hora. Eles são chamados de limites fundamentais e para a gente não ter que ficar resolvendo algo muito complexo toda vez, a gente toma o valor deles como conhecido.
Hoje eu vou te mostrar o limite fundamental trigonométrico:
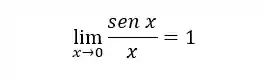
O que eu estou querendo te dizer é que toda vez que você ver um limite com essa carinha aí de cima (x tendendo a zero de seno de x sobre x) você estará diante de um limite fundamental trigonométrico e o resultado vai ser sempre igual a 1.
Como utilizar o limite fundamental trigonométrico?
Como você já deve ter imaginado, resolver questões sobre o limite fundamental trigonométrico não é assim tão fácil… 😥
Acontece que os professores “escondem” o limite fundamental, e você vai precisar manipular os limites até chegar no limite fundamental.
Mas calma, sem desespero, são basicamente 2 manipulações que podem ser feitas:
- Utilizar as propriedades trigonométricas
- Aplicar as propriedades dos limites
- Usar substituições
Exemplo 1
Dá uma olhada nesse limite aqui:
No primeiro momento a gente não consegue ver o limite fundamental.
Mas podemos usar as propriedades trigonométricas, e lembrar que
Olha só quem aparece ali quando utilizamos essa propriedade! Ele mesmo, o limite fundamental trigonométrico.
Agora é só separar os limites, aplicar o limite fundamental trigonométrico e correr pro abraço:
De boas não? Em outros casos, você pode precisar de outras relações trigonométricas, então clica aqui no link pra ver nossa tabela com todas as principais propriedades trigonométricas
Exemplo 2:
Algumas vezes também será necessário fazer uma substituição simples para que o limite fundamental apareça. Olha esse exemplo aqui:
Note que ele se assemelha muito o limite fundamental trigonométrico, mas não é exatamente ele, pois temos
Vamos então substituir
E precisamos também alterar a tendência do limite:
Agora, reescrevendo o limite, temos:
E olha quem apareceu ali!
Agora só resolver tranquilamente:
Irado, não é?
Mas agora você deve estar se perguntando: Como eu vou saber quando usar uma manipulação e quando usar outra?
Bom, isso é só praticando muito com exercícios até pegar o jeito mesmo. Então, bora lá?
Como utilizar o limite fundamental trigonométrico?
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ - Cálculo 1 - PF 2014.1 - 1 a
Calcule:
Passo 1
Temos uma indeterminação do tipo :
Passo 2
Vamos abrir essa tangente em seno sobre cosseno:
Agora é só separar as exponenciais e o cosseno da jogada:
Passo 3
O primeiro vai embora pelo limite fundamental trigonométrico. Já o segundo pode ser substituído de primeira sem indeterminação:
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule o limite, caso exista.
Passo 1
Substituindo teremos indeterminação:
Passo 2
Olha, para esse cara, a princípio, não temos nenhum limite fundamental que possamos aplicar. Agora, tem ali um no denominador e funções trigonométricas que me parece dar a entender que podemos achar um seno a partir desse do numerador.
Então, é o seguinte, vamos lembrar de uma relação da trigonometria:
Po, repara, o numerador do meu limite pode ser multiplicado pelo conjugado dele, ou seja, , para gerar essa relação e ter tudo em função da tangente:
Então multiplicamos esse cara por cima e por baixo da função, para manter a igualdade:
Passo 3
Bom, escrevendo a tangente em função de seno e de cosseno, olha o que teríamos:
Repara, no primeiro termo temos o limite fundamental trigonométrico! No segundo só existem termos que podemos substituir de primeira, lembrando que :
Resposta
Exercício Resolvido #3
Elaboração Própria
Calcule o limite, caso exista.
Passo 1
Substituindo:
Passo 2
Eu não faria ideia de como começar essa questão, não fosse essa diferença de raízes quadradas, que me faz lembrar daquela relação de produtos notáveis:
Onde o meu seria a primeira raiz, a segunda e o que eu tenho ali é um . Vou multiplicar em cima e embaixo por :
Passo 3
Gente, agora basta pegar um desses do no denominador e dividir a tangente e o seno, abrindo ainda a tangente como seno sobre cosseno:
Passo 4
Agora, no primeiro termo do primeiro limite fundamental trigonométrico que apareceu ali temos que abrí-lo pela relação trigonométrica que diz que em cima e embaixo para poder substitituí-lo:
Agora nós podemos Substituir os limites fundamentais trigonométricos por e os valores que não geraram indeterminações. Você vai ver que o único problema é naquele no denominador e o último termo do limite:
Repara que para com indo a nós vamos tender lateralmente pelos dois lados a ! Então sua tendência é para .
Resposta
Exercício Resolvido #4
Elaboração Própria
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Passo 1
Substituindo:
Passo 2
Raciocina comigo: temos ali uma diferença de termos ao cubo, no numerador. Ao cubo? Sim, ao cubo, por que aquele pode ser escrito como . Ora, uma diferença de termos ao cubo pode ser aberta pelo seguinte produto notável:
Nesse caso, o nosso será e .
Passo 3
Agora, aquele termo ali pode ser multiplicado por e através do seguinte produto notável:
Podemos abrir esse cara como:
E talvez você não lembre, mas pela relação fundamental da trigonometria temos o seguinte:
Então é isso, vamos multiplicar o termo no denominador e no numerador por .
Passo 4
Agora a questão é só de simplificar os termos:
Repara que cortando o seno ao quadrado com o seno ao cubo surgiu ali um limite fundamental trigonométrico, com aquele do numerador. Agora é só substituir os valores desse limite e de :
Resposta
Exercício Resolvido #5
Elaboração Própria
Calcule cada limite, quando possível. Caso conclua que o limite não existe, justifique.
Passo 1
Substituindo ficamos com um :
Passo 2
Essa questão depende apenas do encaixe do limite fundamental trigonométrico. Temos um termo dentro do argumento do seno para qual quando vai a . Afinal, . Chamando , teremos na nossa substituição:
Basicamente, é como se tivéssemos o seguinte acontecendo:
Passo 3
OK, dado que esse é o limite fundamental (para ), sabemos o resultado final:
Resposta
Exercício Resolvido #6
Elaboração Própria
Calcule o limite, caso exista.
Passo 1
Se eu substituir caímos numa indeterminação de :
Passo 2
A ideia aqui, então, é forçar aparecer o termo dentro do seno, que está zerando, embaixo dele próprio. No caso, o . Temos ali um seno ao cubo, então vou multiplicar em cima e embaixo por :
Passo 3
Vou separar os limites fundamentais do resto:
Passo 4
Para resolver o primeiro limite precisamos de uma substituição . Nesse caso,
Substituímos o Limite Fundamental Trigonométrico no primeiro termo e o no segundo:
Resposta
Exercício Resolvido #7
Elaboração Própria
Calcule o limite abaixo. Justifique suas respostas.
Passo 1
Substituindo:
Passo 2
Seguinte, vamos começar abrindo todos esses termos do segundo grau:
O que ficaria mais ou menos assim:
Passo 3
Cara, repara que aquele seno está indo para e que o logo embaixo dele também vai a . Poxa, se o termo dentro do seno fosse igual ao que ele está sendo dividido, poderíamos usar o Limite Fundamental, não é?
Para chegar nisso então, vamos multiplicar o termo em cima e embaixo por :
Ali no denominador, o para debaixo do seno e tiro um dos .
Passo 4
Separamos o limite todo em dois:
Para o primeiro, vamos fazer que
o que gera:
Quando . Assim:
Com isso, basta analisar o outro limite e teremos o nosso resultado:
Vemos que, por zerar o denominador, o limite terá tendências diferentes dependendo de qual lado nos aproximamos. De qualquer jeito, ele não existirá, pois explode para mais ou menos infinito.
Resposta
Exercício Resolvido #8
UFF, Cálculo IA-Lista 5, GMA, 2008-1, Questão 12.
Calcule o limite, se possível. Caso conclua que o limite não existe, justifique.
Passo 1
Antes de tudo, quero só dizer que essa questão não é fácil, mas vamos explicá-la com calma.
Ao substituir já vemos um belo :
Passo 2
Primeira coisa, já é usual ver um cara desses com diferença de quadrados. Vamos abrir logo, com o produto notável:
Separei o do resto pois ele vai convergir para um valor. Substituindo ele:
Agora podemos nos concentrar no que sobrou:
Passo 3
Vai parecer meio aleatório (e é mesmo...), mas eu vou fazer uma substituição com o termo do denominador. Eu não tenho muito o que fazer, então vou pegar o cara que se destaca e substituí-lo por :
Com isso, teremos:
Passo 4
Eu sei que não parece ter melhorado muito, mas existe uma propriedade para o seno de uma diferença de ângulos, essa aqui:
Se eu fizer essa com o seno ali de cima, terei:
Temos que e . Logo,
Voltando no limite, olha que beleza:
Passo 5
Multiplicando em cima e embaixo por , teremos, fazendo uma segunda substituição de , com :
Apareceu o Limite Fundamental Trigonométrico. Substituindo-o:
Certo, com isso o resultado final fica:
Resposta
Exercício Resolvido #9
Hamilton Luiz Guidorizzi, Um curso de cálculo Volume I, 5ª ed. Rio de Janeiro: LTC, 2001, pg.97, 3d.
Calcule:
Passo 1
Vamos lá! Primeira coisa que a gente vai fazer vai ser substituir x por p e ver o que que esse limite vai dar pra gente!
Para esse cara temos uma indeterminação de . E agora, o que que a gente faz então?
Pra desfazer essa indeterminação, vamos ter então que manipular as expressões do numerador e do denominador matematicamente de forma que a gente consiga desfazer a indeterminação.
Então a primeira coisa que a gente pode fazer é transformar essas secantes em expressões com cossenos:
Show de bola, agora a gente tem mais coisa pra trabalhar, beleza? Vamos continuar mexendo ai pra resolver o nosso limite!
Passo 2
Como esses cossenos do denominador não vão gerar indeterminação, então vou separá –los do limite principal:
Uma outra coisa que a gente pode fazer é pegar esse e o substituir por uma variável auxiliar , isso só no primeiro limite. Ficaria assim,
Agora com esse a gente vai ter outras relações trigonométricas pra trabalhar em cima!
Passo 3
Agora vamos abrir o segundo cosseno pela seguinte propriedade trigonométrica:
Como temos uma soma fica:
Dando uma arrumada, ele vai parecer beeem mais fácil de sair:
A gente pode separar isso como a soma de dois limites. E também, como nosso limite está calculado em , podemos colocar o que é função de pra fora do limite. A nossa expressão arrumadinha vai ficar assim então:
Passo 4
Olhando pro primeiro limite, que que a gente vai poder fazer nele? Afinal o denominador ainda está indo pra zero...
A gente pode multiplicar ele pelo seu conjugado, em cima e embaixo:
Vale lembrar que , ou seja, :
Separando temos:
Substituímos no primeiro limite o Limite Fundamental Trigonométrico, no segundo podemos apenas substituir :
Ufa, acabamos uma parte!
Agora falta resolver e resolver .
Aguenta ai que tá quase!
Passo 5
Esse outro limite também sai no Limite Fundamental Trigonométrico:
Então relembrando, a gente tinha aberto nosso limite inicial em:
Ai depois que abrimos ficamos com:
Essa primeira parte a gente já resolveu!
Agora substituindo por no limite:
Ufaaa, até que enfim, agora acabou!