4. Calcular , onde é o retângulo , . Interpretar geometricamente.
Passo 1
Falaee, beleza??
Queremos resolver a seguinte integral:
Onde os intervalos dados são:
E
Em outras palavras, queremos resolver a seguinte integral dupla:
Para isso, basta primeiro respondermos com relação a e, em seguida, com relação a !!
Passo 2
Vamos começar resolvendo com a integral mais interna:
Podemos aplicar a propriedade da soma de integrais. Assim, ficamos com:
Resolvendo as integrais:
Aplicando os limites de integração:
Agora vamos aplicar na integral mais externa!!
Passo 3
Aplicando na integral mais externa:
Resolvendo a integral:
Aplicando os limites de integração:
Logo, concluímos que:
Passo 4
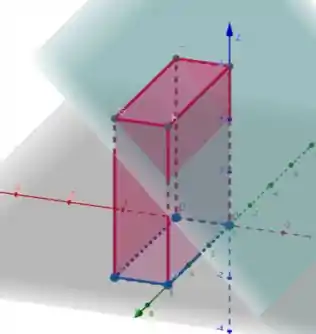
Tendo a seguinte representação geométrica:
No plano , temos o retângulo que vai de a e de a .
Acima desse retângulo, o plano cresce linearmente com , de (quando ) a (quando ).
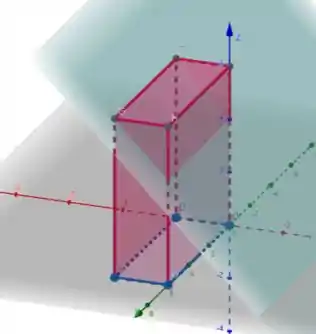
Com área igual a .
Resposta