Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.2 - Ex. 28
Determine o volume do sólido limitado pelo paraboloide elíptico , pelos planos e e pelos planos coordenados.
Passo 1
Fala, pessoal! Tranquilo?
A questão pede para acharmos o volume abaixo de:
Nós sabemos que o volume de um sólido é dado por:
Onde:
O próprio enunciado já nos dá a função:
Então, para calcular nossa integral dupla faltam os limites de integração em e em . Esses limites vêm da região abaixo da função, no plano . Plotando a região que o enunciado dá, teremos:
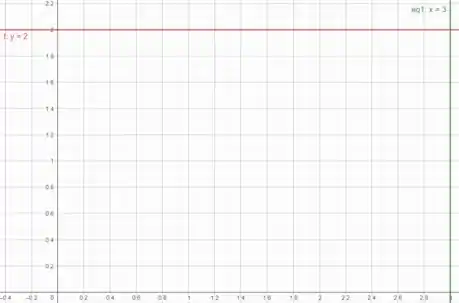
Onde os planos coordenados no plano são os eixos e . Então vemos que nossos limites serão:
Para calcular o volume abaixo de uma superfície, só precisamos fazer uma integral dupla, onde esse retângulo são nossos limites, e a superfície é nossa função. Desse jeito
Lembrando que isso é o mesmo que
Mãos à obra!
Passo 2
Então a gente pode resolver separadamente, começando por:
Que é a integral de dentro. Aqui vamos considerar como constante. Lembrando sempre que a integral da soma é a soma das integrais, então vamos reescrever essa integral
Beleza, vamos por partes, começar resolvendo a primeira integral
Essa foi rápida. Agora vamos para próxima:
Como a gente só está integrando em , é uma constante, então podemos tirar da integral
Aplicando os limites de integração:
Beleza, só falta uma agora!
Vamos começar tirando a constante da integral:
Resolvendo a integral, ficamos com:
Aplicando os limites
Substituindo os resultados que achamos:
Passo 3
Podemos integrar em agora
Olha só! Temos outra integral de uma soma! Vamos usar a mesma propriedade, a integral da soma é a soma das integrais.
Vamos integral por integral de novo:
Aplicando os limites de integração:
Agora vamos para a segunda integral, talvez essa seja a mais complicada que vamos fazer:
Vamos começar colocando a constante para fora da integral:
Agora vamos fazer uma substituição de variáveis, para facilitar nosso cálculo. Chamando parte da função de :
Integrando :
Então, substituindo:
Resolvendo a integral:
Voltando da substituição:
Agora só aplicar os limites de integração:
Agora só falta a última integral, onde já vamos começar colocando a constante para fora:
Resolvendo integral:
Aplicando os limites de integração:
Agora é só substituir os resultados:
Então finalmente achamos o nosso volume: