Encontre a área da regiao sombreada, onde .
Passo 1
Fala aí, pessoal!
Em coordenadas polares temos que a área de uma região é dada pela integral
onde r é a função que determina como o raio da curva varia em relação ao ângulo no intervalo .
No caso, como temos a forma da integral apresentada, basta sabermos a função a ser integrada e seus limites para realizarmos o cálculo e obter o resultado pedido pela questão.
A região sombreada está presente na imagem
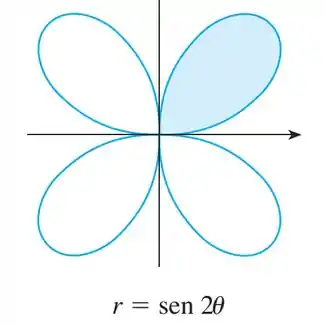
Passo 2
Em primeiro lugar, vamos montar nossa integral.
Temos que a função apresentada pela questão é .
O intervalo de integração é dado por , pois na figura apresentada no passo 1 podemos ver que a região sombreada se encontra no primeiro quadrante.
A integral a ser resolvida, portanto, é dada por
Passo 3
Teremos então
Para resolvermos essa integral, basta calcularmos da forma que faríamos em uma integral usual em coordenadas cartesianas.
Precisamos utilizar a fórmula fundamental da trigonometria e a soma de arcos para reescrever o integrando
Utilizando essas relações, podemos obter
Passo 4
Realizando essas substituições, temos para resolver a integral
Integrando as funções, temos
Com isso conseguimos chegar ao resultado, pessoal!
Resposta
Logo, a resposta é