Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 34
Encontre a massa e centro de massa de um hemisfério sólido com raio se a densidade em qualquer ponto for proporcional à sua distância da base.
Passo 1
Faala pessoal, tudo bem?
Nessa questão, a gente precisa encontrar a massa e o centro de massa de um sólido.
Pra isso, temos fórmulas para a massa:
E para as coordenadas do centro de massa :
Onde:
- é o sólido que estamos trabalhando.
- é a função densidade. Ela retorna a densidade do sólido em um determinado ponto .
Para o caso do nosso problema, já sabemos que é um hemisfério (ou seja, metade de uma esfera). Pra simplificar a explicação, vamos assumir que esse hemisfério é a parte de cima () de uma esfera centrada na origem.
Além disso, o problema diz que “a densidade em qualquer ponto for proporcional à sua distância da base”. Vamos usar disso pra definir:
Onde é uma constante de proporcionalidade e é a distância de um ponto até a base do sólido.
Vamos começar a questão descobrindo quem é esse , através do esboço do sólido. Depois, vamos definir ele em coordenadas esféricas (como nosso sólido é parte de uma esfera, faz sentido fazermos isso né?):
A variável que normalmente chamamos de , vamos usar , pra não confundir com a função densidade!
Daí, podemos transformar nossas integrais em integrais iteradas e calcular!
Passo 2
Bom, vamos começar vendo um esboço do nosso sólido.
Ele é a parte de cima de uma esfera centrada na origem e de raio :
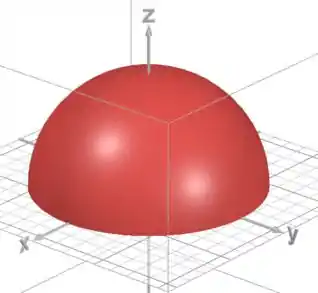
Essa base que a questão fala coincide com o plano ! É o plano quadriculado nessa figura.
Então a distância de um ponto qualquer pra essa base vai ser a altura do ponto, ou seja, sua coordenada . Assim:
Passo 3
Para definir o nosso sólido com coordenadas polares, vamos usar as definições de cada uma das variáveis polares.
O é a distância de um ponto até a origem. Como estamos em uma esfera de raio centrada na origem:
O é a angulação entre a reta que liga o ponto e a origem e o eixo . Na prática, se o ponto está na parte positiva de e se está na parte negativa. No nosso caso, pegamos todos os pontos da esfera na parte positiva de , então:
Por último, para vermos o , a gente olha a projeção do sólido no plano , que vai ser um disco de raio :
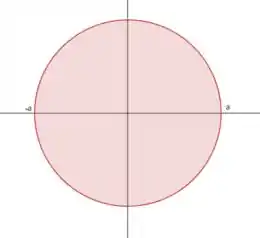
Esse é o mesmo do sistema de coordenadas polares. Como a projeção no plano é o disco inteiro:
A gente não pode esquecer que sempre que fizermos uma mudança de variáveis, precisamos incluir o jacobiano! Nesse caso, .
Nos próximos passos, vamos transformar todas as integrais em integrais nesse sistema de coordenadas. Os limites de integração, então, vão ser:
Passo 4
Vamos começar as contas!
Para o cálculo de :
Passando para coordenadas esféricas:
A gente vai integrar de dentro pra fora.
Começando em função de , considerando e constantes:
Como o integrando todo só depende de e , ele pode sair dessa primeira integral:
Depois, vamos integrar em função de , mantendo constante:
O termo é uma constante e pode sair da integral inteira. Já é constante em função de e sai dessa integral. Fica assim:
Vamos mexer um pouco com esse integrando. Pela fórmula de , temos:
Então:
E como a primitiva de é :
Como e :
E por último integramos em função de :
Passo 5
Agora vamos calcular as coordenadas do centro de massa. Começando com :
Em coordenadas esféricas:
Vamos arrumar um pouco essa integral antes de começar a integrar. Como é constante, ele sai da integral. E vamos juntar os termos que dependem de cada variável:
Agora vamos começar a integrar, em função de , com e constantes:
Como é constante, pode sair dessa primeira integral:
Só que , então a diferença entre os dois vai dar zero:
Passo 6
Agora vamos calcular o , que vai acontecer alguma coisa parecida...
Em coordenadas esféricas:
Da mesma forma que arrumamos a última integral, essa fica assim:
Jogando pra fora da primeira integral, pra integrarmos em função de :
De novo, como :
Passo 7
Por último, o (não se anima que esse não vai dar zero 😪):
Mudando pra coordenadas esféricas:
Arrumando:
Primeiro integrando em função de , com e constantes. Vamos tirar o integrando todo dessa primeira integral porque não depende de :
Agora, vamos integrar em função de , com constante. Então podemos tirar dessa integral e da integral toda:
Vamos fazer uma substituição :
Então:
Integrando em função de :
Pra terminar, integramos em função de . Podemos tirar o da integral:
Ou seja,