Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 5

Nos Exercícios 1-8, descreva a região dada em coordenadas polares.

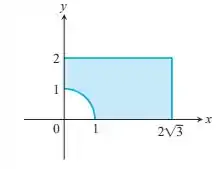
Passo 1

Faaaala, cara! Tranquileba?

Das coordenadas polares temos que:

x = r cos ⁡ θ

y = r   s e n θ

x 2 + y 2 = r 2

E em caso de dúvidas, vejamos a figura para que possamos entender melhor.

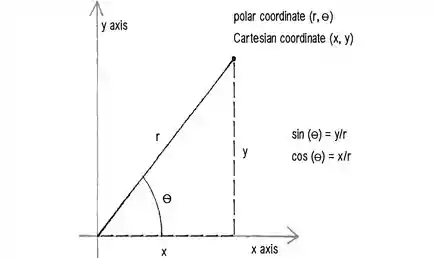
Passo 2

Da figura, nós temos 2 retas e uma circunferência, isto é:

x = 2 3

y = 2

x 2 + y 2 = 1

Passo 3

Assim:

Para:

x 2 + y 2 = 1

r = 1

Para:

y = 2

r   s e n θ = 2

r = 2 s e n θ = 2   c o s s e c ( θ )

Para:

x = 2 3

r cos ⁡ θ = 2   3

r = 2 3   s e c ( θ )

De modo que:

2 3 s e c θ = 2 cossec ⁡ θ

c o s s e c θ sec ⁡ θ = 1 s e n θ 1 cos ⁡ θ = cos ⁡ θ s e n θ = t g - 1 ( θ )

t g - 1 θ = 3

θ = π 6

Assim:

0 ≤ θ ≤ π 6

1 ≤ r ≤ 2 3 sec ⁡ θ

E:

π 6 ≤ θ ≤ π 2

1 ≤ r ≤ 2 3   c o s s e c θ

Resposta

0 ≤ θ ≤ π 6

1 ≤ r ≤ 2 3 sec ⁡ θ

E:

π 6 ≤ θ ≤ π 2

1 ≤ r ≤ 2 3   c o s s e c θ

Exercícios de Livros Relacionados

Calcular ∬ R x - 1 2 + y - 2 2 d x d y , onde R é delimitada por x - 1 2 + y - 2 2 = 1 .
Calcular ∬ R x y d x d y , onde R é delimitada por x 2 4 + y 2 9 = 1 .
Calcular ∬ R ln ⁡ ( x 2 + y 2 ) d x d y , sendo R o anel delimitado por x 2 + y 2 = 16 e x 2 + y 2 = 25 .
Calcular ∬ R y d x d y , sendo R o círculo x 2 + y 2 - 4 y ≤ 0 .
Calcular ∬ R ( 8 - x - y ) d x d y , sendo R delimitada por x 2 + y 2 = 1 .