1. Queremos encontrar as soluções da equação diferencial que são constantes, para isso precisamos que , portanto:

ou

Então são soluções constantes da equação , e

Passo 2

2. Precisamos determinar para quais valores de y a nossa função será crescente. Para que isso aconteça precisamos que . Então,

Como é sempre maior que 0, precisamos apenas analisar o caso em que

Podemos descobrir esse intervalo facilmente ao olharmos o gráfico de , onde o eixo horizontal corresponde ao eixo y e o vertical ao eixo t.



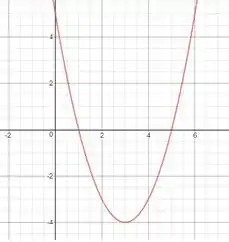
Com isso, podemos concluir que quando ou . Então a função está aumentando justamente quando e , podemos escrever isso também da seguinte forma:

Passo 3

3. Agora nosso objetivo é encontrar para quais valores de a função é decrescente. Ou seja, .

Como , precisamos garantir que para que nossa condição seja satisfeita.

Podemos ver quando isso acontece ao olharmos o gráfico dessa função:

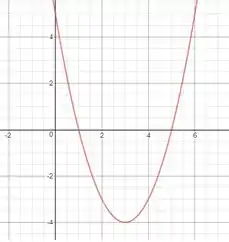
Veja que quando

Então a função y(t) será decrescente quando . Também podemos escrever esse mesmo intervalo como