Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.1 - Ex. 18

Se R = 0,1 × [ 0,1 ] , mostre que 0 ≤ ∬ R sen ⁡ x + y d A ≤ 1 .

Passo 1

E aiii galerinha fera! Tudo na paz!? Bora fazer mais uma!

Vamos entender o enunciado. Ele nos forneceu um intervalo de variação que está na nomenclatura R = 0,1 × [ 0,1 ] , que significa:

R = a , b × c , d ,     a ≤ x ≤ b ,     c ≤ y ≤ d  

Assim sabemos o intervalo de variação de x e y . Sabendo disso, ele pediu para mostrarmos que o resultado da integral dupla de s e n ( x + y ) na região R está no intervalo de [ 0,1 ] :

0 ≤ ∬ R sen ⁡ x + y   d A ≤ 1

Beleza até aqui pessoal!? Como resolvemos isso?

Agora vamos com calma, e montar uma estratégia juntos. Primeiro vamos avaliar a expressão ( x   + y ) na região R , e compreender qual o quadrante no círculo trigonométrico ela representa.

Feito isso, podemos concluir o intervalo de variação da função s e n ( x + y ) , pois sabemos dentro de um quadrante qual a variação do seno.

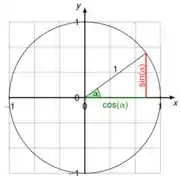
Por exemplo, se nossa soma ( x + y ) estiver no 1º quadrante. Sabemos que esse intervalo corresponde a variação do 0 ≤ s e n ( α ) ≤ 1 . Temos que chegar em algo parecido com isso.

Ai na última etapa, aplicamos a integral dupla na região R na expressão que chegamos anteriormente, ficando algo do tipo:

∬ R 0 d A ≤ ∬ R s e n ( x + y ) d A ≤ ∬ R 1 d A

Esse bizu ficou mastigadinho para vocês, ein!? Bora lá gabaritar essa! Vocês são feraaas!

Passo 2

Vamos avalizar a função dada na integral:

s e n   x + y

Observe que temos x + y dentro do s e n , e sabemos o intervalo de variação da região R:

R = 0,1 × [ 0,1 ]

    0 ≤ x ≤ 1 ,     0 ≤ y ≤ 1

Assim, podemos definir um intervalo de variação para x + y , fazendo o primeiro ponto x = 0 e y = 0 , e o segundo ponto como x = 1 e y = 1 .

x + y = 0 + 0 = 0

x + y = 1 + 1 = 2

Agora, temos o intervalo de variação da expressão ( x + y ) , que é:

0 ≤ x + y ≤ 2

Com isso, sabemos que estamos no primeiro quadrante do círculo trigonométrico.

Passo 3

Já a função seno, sabemos que seu valor vai ser maior igual a zero. Porque isso? Devido a soma de ( x + y ) ser positiva. Observe o círculo trigonométrico abaixo:

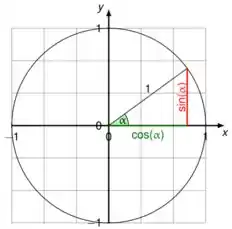
Repare uma coisa. Obtemos antes que ( x + y ) sempre serão positivos, logo sempre estaremos no primeiro quadrante do círculo trigonométrico.

Então,

sen ⁡ θ ≥ 0 para 0 ≤ θ ≤ π 2

Logo, podemos concluir que

f x , y = s e n   x + y ≥ 0 para todo x , y ∈ R

Avaliando o círculo trigonométrico, e fazendo uma comparação entre s e n x + y e s e n ( θ ) podemos compreender qual o intervalo:

0 ≤ s e n x + y ≤ 1

Passo 4

Sabendo o intervalo da função s e n x + y

0 ≤ s e n x + y ≤ 1

Agora, aplicamos integral dupla na região R em todos os termos, temos que:

∬ R 0 d A ≤ ∬ R s e n ( x + y ) d A ≤ ∬ R 1 d A

A integral dupla de zero vai ficar:

∬ R 0 d A = 0

Já a integral dupla de 1 d A na região R :

R = 0,1 × [ 0,1 ]

    0 ≤ x ≤ 1 ,     0 ≤ y ≤ 1

∫ 0 1 ∫ 0 1 1 d A = ∫ 0 1 ∫ 0 1 d x d y

∫ 0 1 x | 0 1 d y = ∫ 0 1 d y

∫ 0 1 d y = y | 0 1 = 1

Logo,

∬ R 1 d A = 1

Assim, temos que

0 ≤ ∬ R s e n ( x + y ) d A ≤ 1

Resposta

Demonstração.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use simetria para calcular a integral dupla. ∬ R x y 1 + x 4 d A ; R = x , y - 1 ≤ x ≤ 1 ; 0 ≤ y ≤ 1 }
Use simetria para calcular a integral dupla. ∬ R 1 + x 2 s e ny + y 2 s e nx d A ; R = - π , π × [ - π , π ]
Calcule a integral dupla.∬_R x s e n ( x + y ) d A ; R = [0 , (pi)/(6)] xx [0 , (pi)/(3)]
Calcule a integral dupla.15. ∬ R tan ⁡ θ 1 - t 2d A ; R = x , y0 ≤ θ ≤ π 3 ;0 ≤ t ≤ 1 2
Determine o volume do sólido limitado pela superfície z = 6 - x y e pelos planos x = 2 , x = - 2 , y = 0 , y = 3 e z = 0 .Use um computador para desenhar o sólido.