Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 23

Para que valor(es) de x teremos e^(- x^2) = x^2 - x + 1 ?

Passo 1

Para obtermos e^(- x^2) = x^2 - x + 1 separaremos em duas funções e vamos plotar o gráfico para ver o ponto de intersecção entre eles. Dessa forma, tomemos y 1 = x^2 - x + 1 e y 2 = e^(- x^2) , plotando o gráfico vamos obter

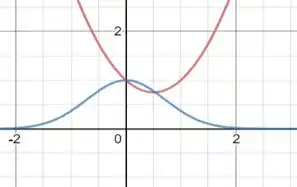
Observamos 2 valores de x para os quais as funções se encontram, o primeiro deles conseguimos encontrar pela observação do gráfico, dando um zoom no mesmo. Assim, encontramos x = 0

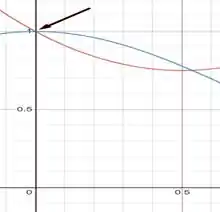
Por fim, para encontrarmos o outro valor de x que que satisfaz a igualdade usaremos o método de Newton para aproximação de raízes que nos diz que

x_n + 1 = x_n - (f ( x_n ))/(f ' ( x_n ))

Passo 2

Primeiramente vamos derivar a função, para poder substituir na fórmula do método de Newton. Assim,

f (x) = e^(- x^2) - x^2 + x - 1 -> f^' (x) = - 2 x e^(- x^2) - 2 x + 1

Agora, precisamos de um ponto inicial x_0 observando o gráfico percebemos que o outro ponto de encontro está próximo de 0.5 = (1)/(2) , então, tomemos esse valor como nosso ponto de partida. Dessa forma,

x_0 + 1 = x_0 - (e^(- x_0^2) - x_0^2 + x_0 - 1)/(- 2 x_0 e^(- x_0^2) - 2 x_0 + 1)

x_1 = (1)/(2) - (e^(- ((1)/(2))^2) - (1)/(2)^2 + (1)/(2) - 1)/(- 2 * ((1)/(2)) e^(- ((1)/(2))^2) - 2 * ((1)/(2)) + 1)

x_1 = (1)/(2) - (e^(- (1)/(4)) - (1)/(4) + (1)/(2) - 1)/(- e^(- (1)/(4)) - 1 + 1)

x_1 = (1)/(2) - (e^(- (1)/(4)) - (1)/(4) - (1)/(2))/(- e^(- (1)/(4)))

x_1 = (1)/(2) - (e^(- (1)/(4)) - (3)/(4))/(- e^(- (1)/(4)))

x_1 = (1)/(2) - ( - 1 + ((3)/(4))/(- e^(- (1)/(4))) )

x_1 = (1)/(2) + 1 - ((3)/(4))/(e^(- (1)/(4)))

x_1 = (3)/(2) - ((3)/(4)) * e^((1)/(4))

x_1 tildetilde 0.536980

Resposta

x = 1 e x tildetilde 0.5 37

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Siga as instruções do Exercício 19, se a = - 2 .
Seja f x = x 4 - x 3 . Mostre que a equação f x = 75 tem uma solução no intervalo [3,4] e use o métdo de Newton para determiná-la.
Seja f x = 3 x - x 3 . Mostre que a equação f x = - 4 tem uma solução no intervalo [2,3] e use o método de Newton para determiná-la.
Deduza o método de Newton a partir de sua interpretação geométrica.
Aplique o método de Newton-Raphson à equação: x 3 - 2 x 2 - 3 x + 10 = 0 com x 0 = 1.9 . Justifique o que acontece.